之前博客介绍了采用双指针法来解决链表类题目Link。
本博文主要介绍用双指针法来解决数组类题目,并且把数组类相关的解题思路也放在此博客中。
数组与链表是最基本的两种数据结构,其他均可以由这两种构成。
链表是用离散的内存块存储数据,而数组是用连续的内存块存储数据。
因此,对于数组,只需要直知道内存空间首地址(也就是数组名),通过索引即可访问任意元素。
在处理数组和链表相关问题时,双指针技巧是经常用到的,双指针技巧主要分为两类:左右指针和快慢指针。
- 左右指针: 两个指针相向而行或者相背而行。
- 快慢指针:两个指针同向而行,一快一慢。
1. 删除有序数组中的重复项

第一次遇到这个题目的时候,还是比较困惑的,主要是返回什么。题目要求是“原地修改”。如果不是原地修改的话,我们直接 new 一个 int[] 数组,把去重之后的元素放进这个新数组中,然后返回这个新数组即可。
而所谓的“原地修改”,其实就是原地删除,不允许 new 新数组,只能在原数组上操作,然后返回一个长度,这样就可以通过返回的长度在原始数组中截取去重后的元素了。
对于此代码,原本有两个解法:
解法1:采用unique函数。时间复杂度O(Nlogn),空间复杂度为O(1)
解法2:采用键值对,时间复杂度为O(n),由于需要一个键值对,空间复杂度估计也是O(n)
而快慢指针法的思路就是:慢指针 slow 走在后面,快指针 fast 走在前面探路,找到一个不重复的元素就赋值给 slow 并让 slow 前进一步。
这样,就保证了 nums[初始点..slow] 都是无重复的元素,当 fast 指针遍历完整个数组 nums 后,nums[初始点..slow] 就是整个数组去重之后的结果。
Click to expand the code. 时间复杂度为O(n),空间复杂度为O(1)
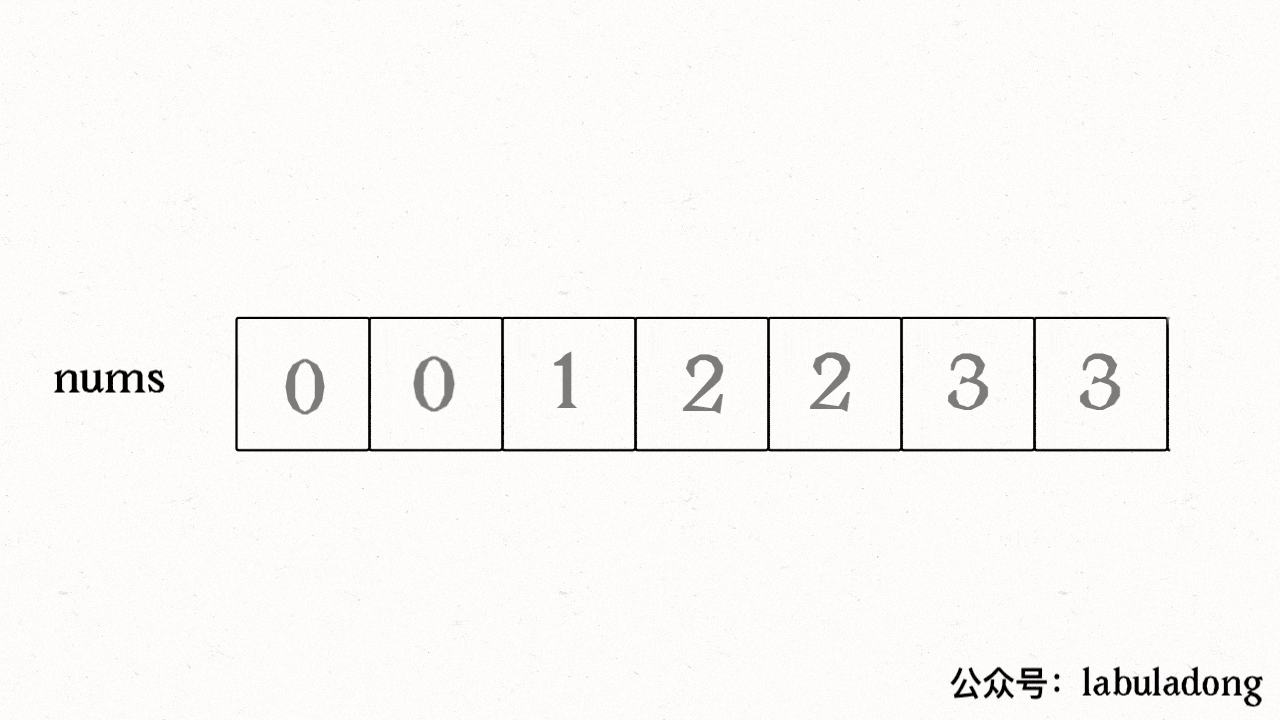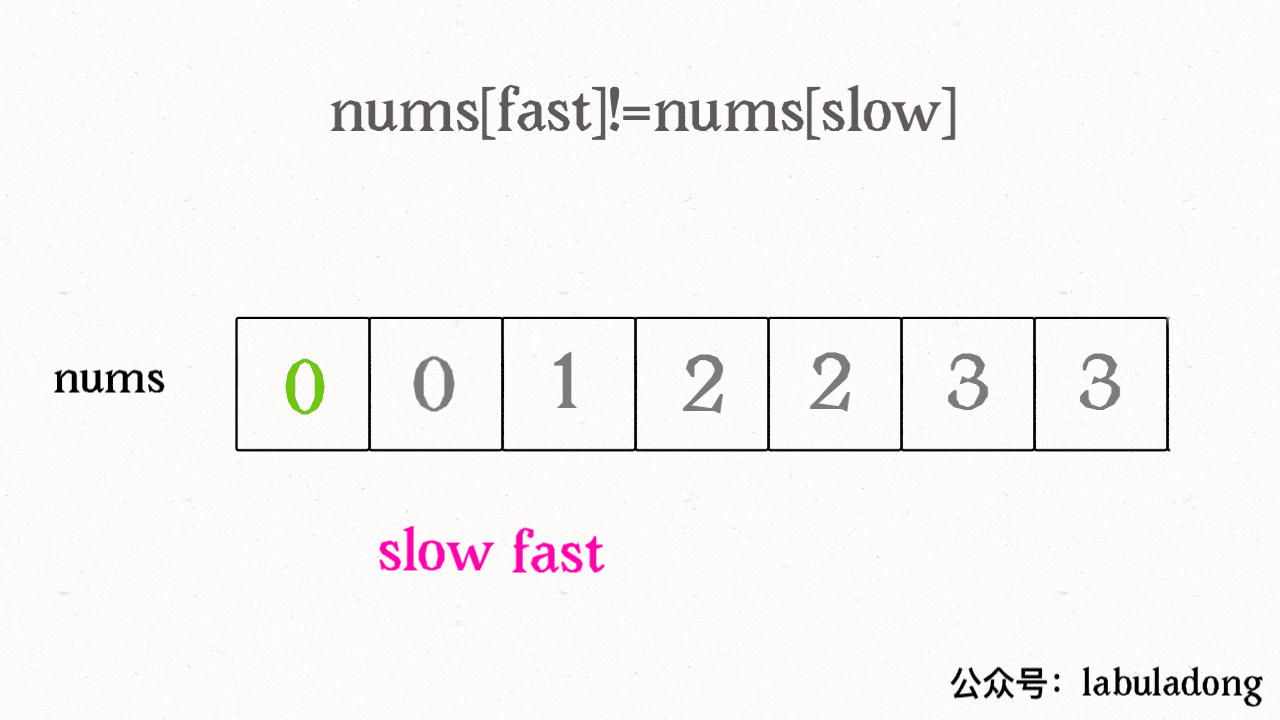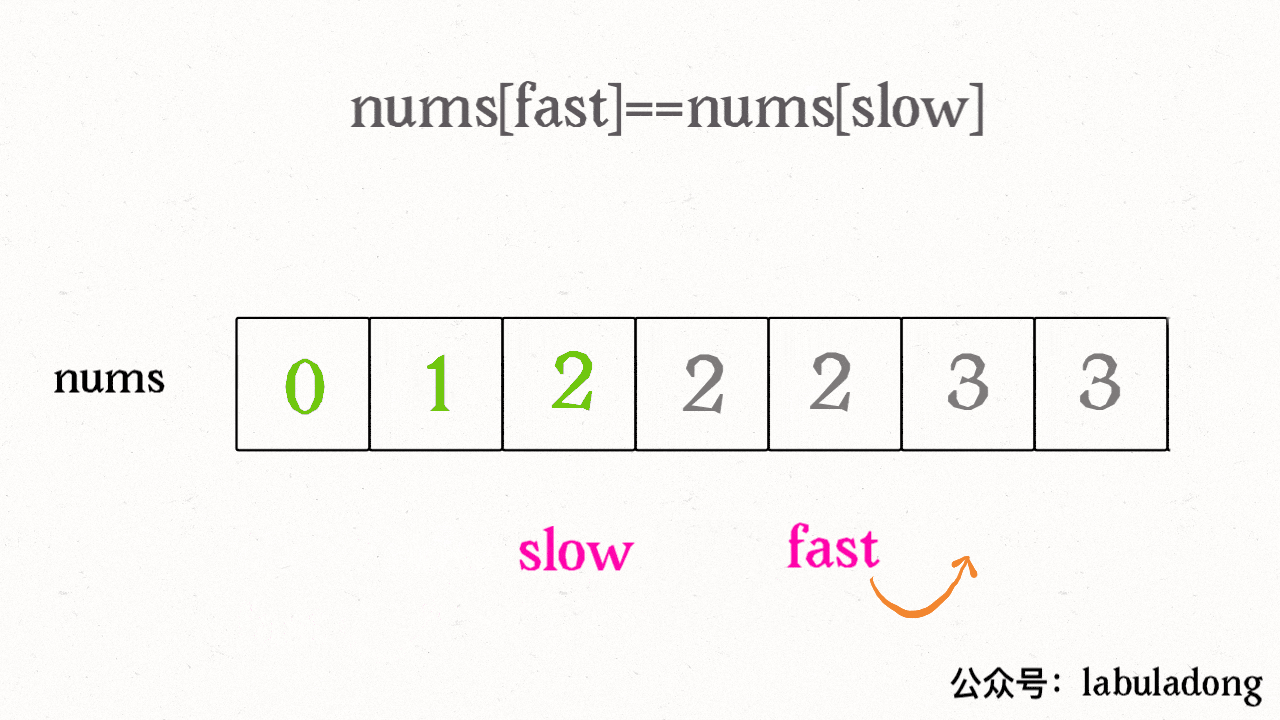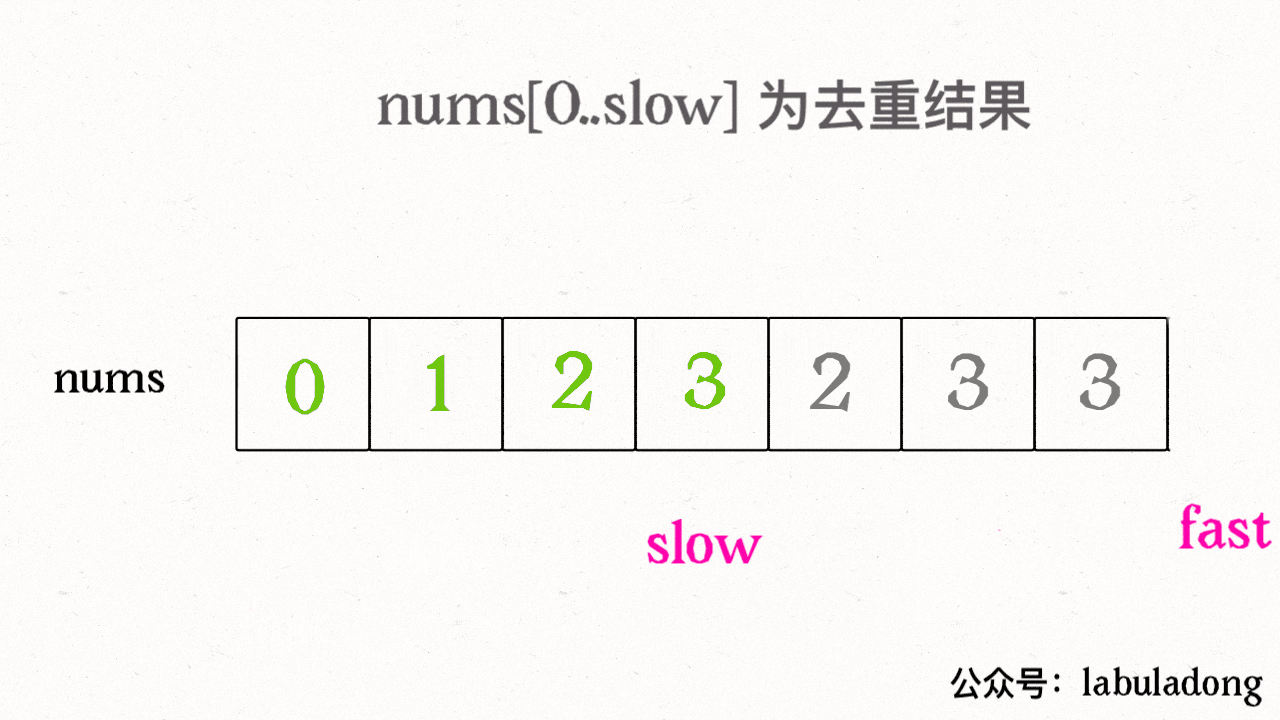
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
//采用双指针法(快慢指针)时间复杂度为O(n),空间复杂度为O(1)
int slow=0, fast=0;
while(fast!=nums.size())//遍历整个数组
{
if(nums[slow]!=nums[fast])//找到不等的
{
slow++;//slow自增(必须先自增,因为一开始fast=slow,下一刻再判断时必须要先把slow自增)
nums[slow]=nums[fast];//进行赋值
}
fast++;
}
//代码将不重复的元素放在数组前面slow索引中~
return slow+1;//这个就是排在前面的不重复的size(注意要+1)
}
};
对于前面的解法1和解法2,特别是解法1,除非比较熟悉cpp的函数,不然一般不懂使用,所以更建议实际解题的时候用算法去解题而不是用库函数取巧🤭
而类似的题目链表类博客中有记录了,给出了两个解法(见Leetcode中83题)
2.移除元素(原地删除而非上面的换位置)

解法1:数组函数的使用,时间复杂度O(Nlogn+N);空间复杂度O(1)
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
// 先进行排序,排序后只需要对找到对应值的位置进行删除即可
sort(nums.begin(),nums.end());//时间复杂度为O(nlogn)
auto index=find(nums.begin(),nums.end(),val);//返回的是指针(时间复杂度为O(n))
if(index!=nums.end())//代表找到了
{
//从找到的位置开始,到结尾
for(auto it=index;it!=nums.end();)
{
if(*it==val)
{
it = nums.erase(it);//直接删掉
}
else
break;
}
}
return nums.size();//返回的是nums 中与 val 不同的元素的数量
}
};
解法2:快慢指针,其实跟上面题1的思路是一样的。时间复杂度为O(n),空间复杂度为O(1)
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int slow=0, fast=0;
while(fast!=nums.size())
{
if(nums[fast]!=val)//不等
{
nums[slow]=nums[fast];
slow++;
}
fast++;
}
return slow;
//此处与有序数组去重的解法有一个细节差异:
// 先给 nums[slow] 赋值然后再slow++
// nums[0..slow-1] 是不包含值为 val 的元素的,最后的结果数组长度就是 slow
}
};
3.移动零
类似上面的解法,只是改为vector以及没有返回值。时间复杂度为O(n),空间复杂度为O(1)
class Solution {
public:
void moveZeroes(vector<int>& nums) {
// 快慢指针
int slow=0,fast=0;
while(fast!=nums.size())
{
if(nums[fast]!=0)//若不为零
{
nums[slow]=nums[fast];
slow++;
}
fast++;
}
while(slow!=nums.size())
{//由于没有返回值,把后面的也赋值为0(因为可能是原本位置的其他值,上面并不是交换操作)
nums[slow]=0;
slow++;
}
}
};
4. 两数之和

左右指针,时间复杂度应该为O(N),空间复杂度应该为O(1)
class Solution {
public:
vector<int> twoSum(vector<int>& numbers, int target) {
// 由于数组已经按照非递减顺序排序,故此可以用左右指针法
int left=0, right=numbers.size()-1;
while(left<right)
{
int sum=numbers[left]+numbers[right];
if(sum==target)//找到了
{
return vector<int>{left+1, right+1};//索引从1开始
}
else if(sum<target)
{
left++;//让值大一些
}
else if(sum>target)
{
right--;//让值小一些
}
}
return vector<int>{ -1, -1};//找不到
}
};
用hash table (时间复杂度为O(N))
class Solution {
public:
vector<int> twoSum(vector<int>& numbers, int target) {
int value_a,value_b;
vector<int> result;
// 用hash table (时间复杂度可以降为O(N))
unordered_map<int, int> hash_able;//(具体的值、坐标)
for(int i=0;i<numbers.size();i++)
{
auto it=hash_able.find(target-numbers[i]);//寻找这个值的另一半
// 如果找到了,
if(it!=hash_able.end())
{
int index_1=it->second;
int index_2=i;
// 注意返回的为坐标值(且下标开始为1)
result.push_back(index_1+1);
result.push_back(index_2+1);
break;
}
hash_able[numbers[i]]=i;//若没找到,就继续放入hash table
}
return result;
}
};
相类似的题目还有下题(几乎一样,只是下标索引从1开始):
解法1:用hash table (时间复杂度为O(N))
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
int value_a,value_b;
vector<int> result;
// 用hash table (时间复杂度可以降为O(N))
unordered_map<int, int> hash_able;//(具体的值、坐标)
for(int i=0;i<nums.size();i++)
{
auto it=hash_able.find(target-nums[i]);//寻找这个值的另一半
// 如果找到了,
if(it!=hash_able.end())
{
int index_1=it->second;
int index_2=i;
// 注意返回的为坐标值
result.push_back(index_1);
result.push_back(index_2);
break;
}
hash_able[nums[i]]=i;//若没找到,就继续放入hash table
}
return result;
}
};
解法2: 暴力匹配的解法(时间复杂度为O(N^2))这必然非最优解了🤭
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
int value_a,value_b;
vector<int> result;
// 暴力匹配的解法(时间复杂度为O(N^2))
for(int i=0;i<nums.size();i++)
{
value_a=nums[i];
for(int j=i+1;j<nums.size();j++)
{
value_b=nums[j];
if(value_a+value_b==target)
{
result.push_back(i);
result.push_back(j);
break;
}
}
}
return result;
}
};
5.反转数组

最简单的就是采用reverse函数了~时间复杂度O(n)
class Solution {
public:
void reverseString(vector<char>& s) {
//采用reverse函数
reverse(s.begin(),s.end());
}
};
但是还是采用双指针法来看看,时间复杂度O(n),空间复杂度为O(1)跟上面一样
class Solution {
public:
void reverseString(vector<char>& s) {
int left=0, right=s.size()-1;
while(left<right)//等于的时候不处理了
{
char temp=s[left];//用个中间变量来赋值~
s[left]=s[right];
s[right]=temp;
left++;
right--;
}
}
};
6.最长回文子串

回文子串的判断应该是经典的动态规划的题目,但是复杂度是O(N^2)。空间复杂度是O(N^2)(存储动态规划状态需要的空间。)
class Solution {
public:
string longestPalindrome(string s) {
int max_length=1;//最长的长度
int begin_index=0;//起始的index
// 动态规划
// 对于坐标为i~j的子串,是否回文子串,状态为dp[i][j]
bool dp[s.size()][s.size()]; //定义动态规划的状态矩阵大小
//确定初始状态,所有长度为1的都是回文子串
for(int i=0;i<s.size();i++)
{
int j=i;
dp[i][j]=true;
}
//进行递推状态转移
// for(int i=0;i<s.size();i++)
for(int i=s.size()-1;i>=0;i--)//要从小到大!!!
{
for(int j=i+1;j<s.size();j++)//j=i的情况以及是初始化了
{
if(s[i]==s[j])//如果相等,那么就检查下一个状态
{
if(j<=i+2)//如果此时到达边界(aba)或(aa)的情况
dp[i][j]=true;
else//继续递推
dp[i][j]=dp[i+1][j-1];
}
else//如果不等,那么当前就是false
dp[i][j]=false;
//如果是回文子串且长度大于记录值
if(dp[i][j] && j-i+1>max_length)
{
begin_index=i;
max_length=j-i+1;
}
}
}
return s.substr(begin_index,max_length);//字符串的截取
}
};
采用双指针解法,时间复杂度是O(N^2)更上面一样的。但空间复杂度更小,为O(1)
class Solution {
public:
// 对于以left与right为中心的最长回文子串
// 通过左右指针向两边扩散
string function(string s, int left, int right)
{
//确保不越界以及相等
while(left>=0 && right<s.size() &&s[left]==s[right])
{
left--;
right++;
}
//若不等的话,会跳出来。所以应该是当前的left+1到right为目标结果
return s.substr(left+1,right-(left+1));
}
string longestPalindrome(string s) {
string result="";
for(int i=0;i<s.size();i++)
{
//以i为中心的,奇数字符串
string s1=function(s,i,i);
//以i为中心的,偶数字符串
string s2=function(s,i,i+1);
// 保存最长的
result= result.size()>s1.size()? result:s1;
result= result.size()>s2.size()? result:s2;
}
return result;
}
};
下面是几乎一样的题目
Click to expand the code。先给出双指针解法,跟上面几乎一样~
下面是动态规划的解法,还是双指针法比较简单,建议实际用双指针法解决~
下面的动态规划解法更容易理解些~
采用二分法来解数组类题目
二分法其实就是左右双指针法的一种特殊情况,即两个指针分别指向数组的两端,然后根据题目的要求,每次将指针移动到中间,然后根据中间的值来判断下一步应该移动哪个指针。 更多关于二分法的介绍请见博客Link。
采用滑动窗口算法来解数组类题目
调滑动窗口算法的快慢指针特性:left 指针在后,right 指针在前,两个指针中间的部分就是「窗口」,算法通过扩大和缩小「窗口」来解决某些问题。 更多关于滑动窗口算法的介绍请见博客Link。
三数之和

先确定一个值,另外两个通过左右指针的方式获取
Click to expand the code。解法2也是双指针
最接近的三数之和

Click to expand the code。有时做最大最小值记录的时候,可以选择初始化为INT_MIN和INT_MAX
四数之和

Click to expand the code。最直接的方法就是用回溯算法。但是运行会超时。230 / 294 个通过的测试用例
Click to expand the code。要避免超时应该采用的是双指针法,类似三数之和。在三数和的基础上上再套一层for循环.注意测试样例中存在long数据。时间复杂度为O(N3)
高效解决接雨水问题
接雨水

Click to expand the code。首先给出暴力的解法。这个思路是最直接的,把问题进行分解然后解题,但是最终只有320 / 323 个通过的测试用例 时间复杂度应该是O(N2)
Click to expand the code.通过备忘录,先预先计算每个i的两个数组,避免每次循环都重复遍历,可以将时间复杂度降低为O(N),空间复杂度为O(1)
Click to expand the code.下面通过双指针法解题,将时间复杂度一样为O(N),如下图所示
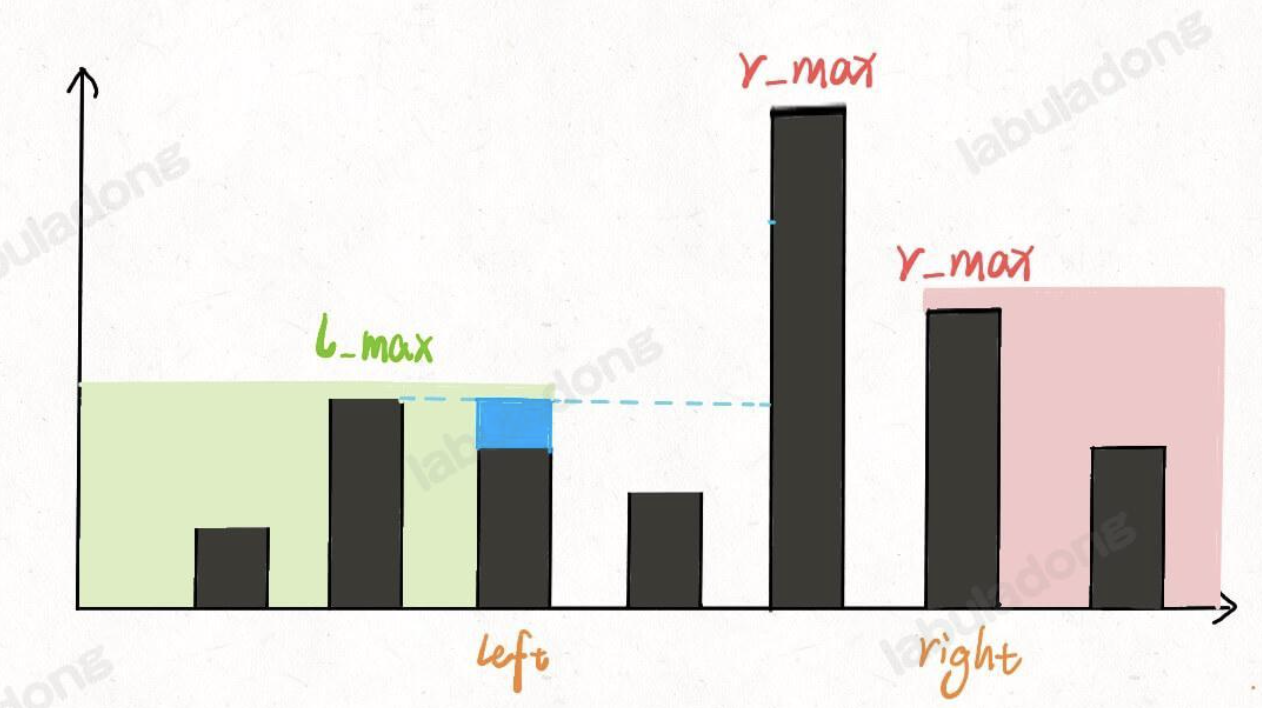
盛最多水的容器
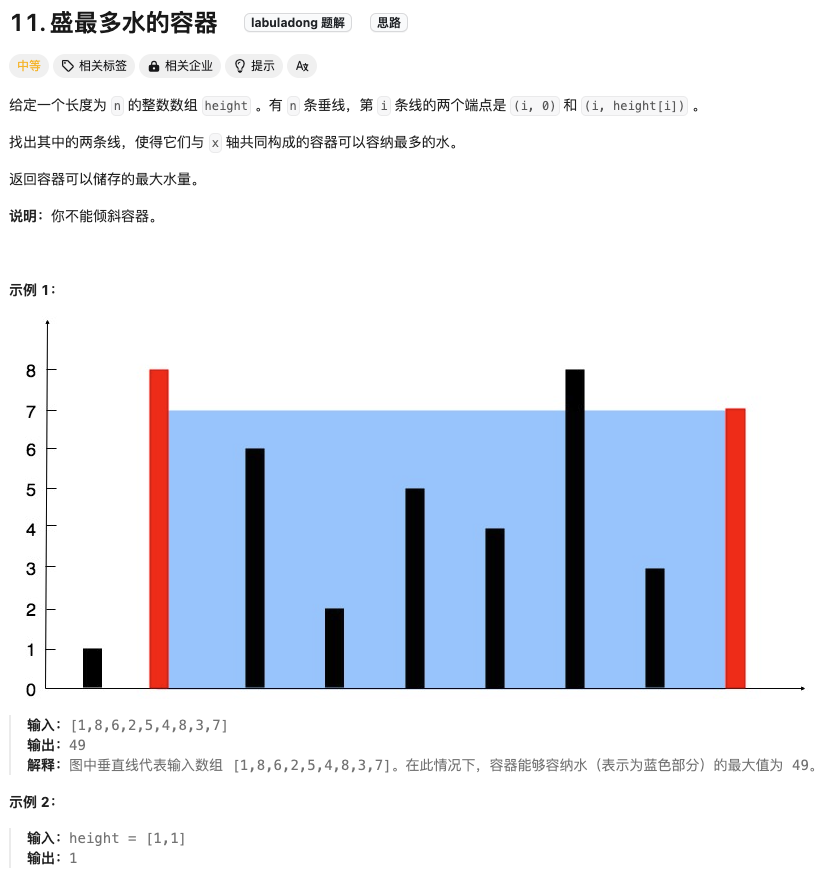
Click to expand the code。上一题给出的类似一幅直方图,每个横坐标都有宽度,而本题给出的每个横坐标是一条竖线,没有宽度。因此就不存在height[i]存放多少水的问题。
因此本题只需要知道了两个指针的位置,就可以计算出最大的面积:min(height[left], height[right]) * (right - left)
Click to expand the code下面写法是一样的。注意更新的索引不要写错了~