引言
从事SLAM领域的研发已经接近5年了,但是对于一些基础的概念和知识点仍然不够清晰。因此,我决定写一篇博客来总结一下视觉SLAM的基础知识,主要为了巩固相关的知识体系。
本博文的内容主要参考了《SLAM十四讲》和视觉SLAM入门系列文章。其余参考资料也会在文末列出。
本博文仅供本人学习记录用,不做任何商业用途。
视觉SLAM目前主要有两大方向:基于学习的方法和基于几何的方法。本博文主要介绍基于几何方法的视觉SLAM。而learning-based的其实也是以几何的方法为基础,更多关于learning-based VO/SLAM的介绍请见博客Link.

Perspective Projection Model
对于视觉SLAM,首先肯定是先需要了解相机的成像模型的,这里用下图直观显示:
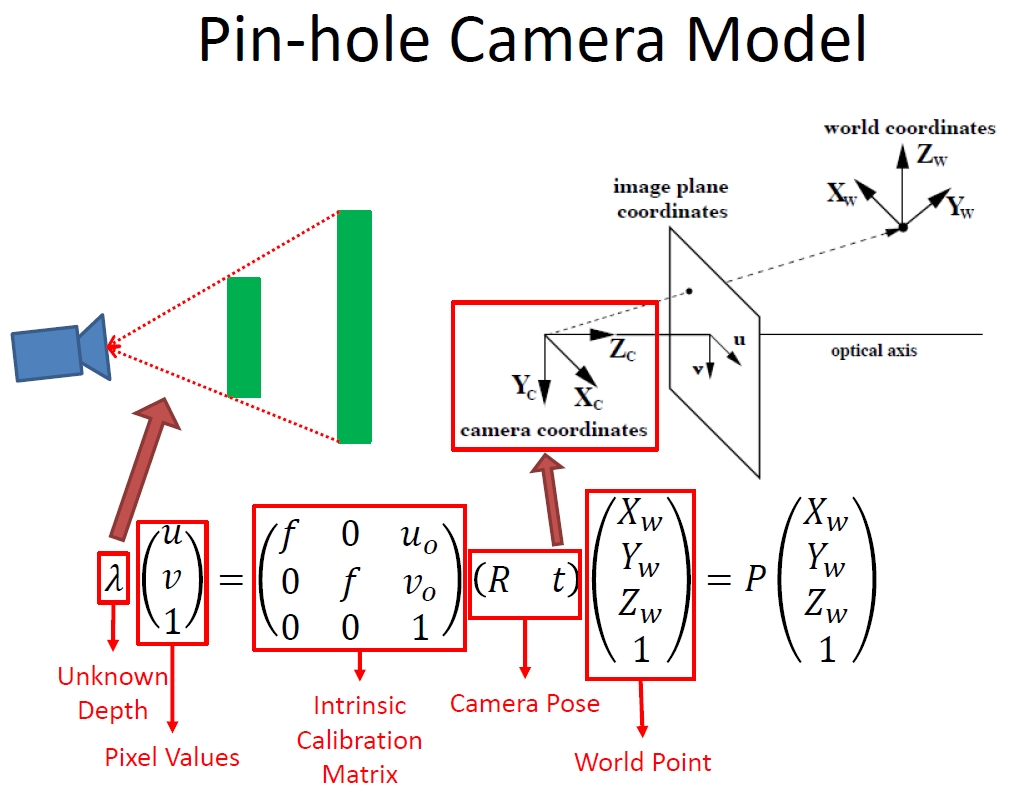
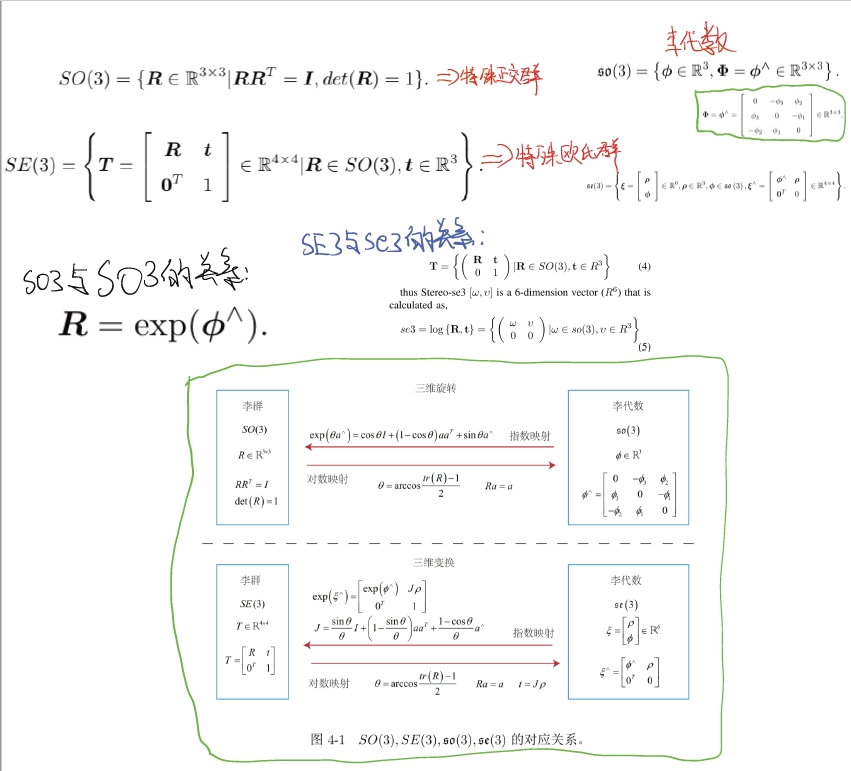
李群与李代数
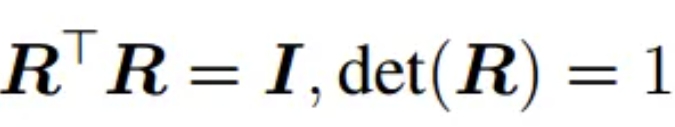
对于变换矩阵T(包含旋转R与平移t),所在的空间为SE(3)(称呼为李群,也就是特殊欧氏群),进行映射为se(3),也就是李代数。 李代数对应李群的正切空间,它描述了李群局部的导数。见下面公式:
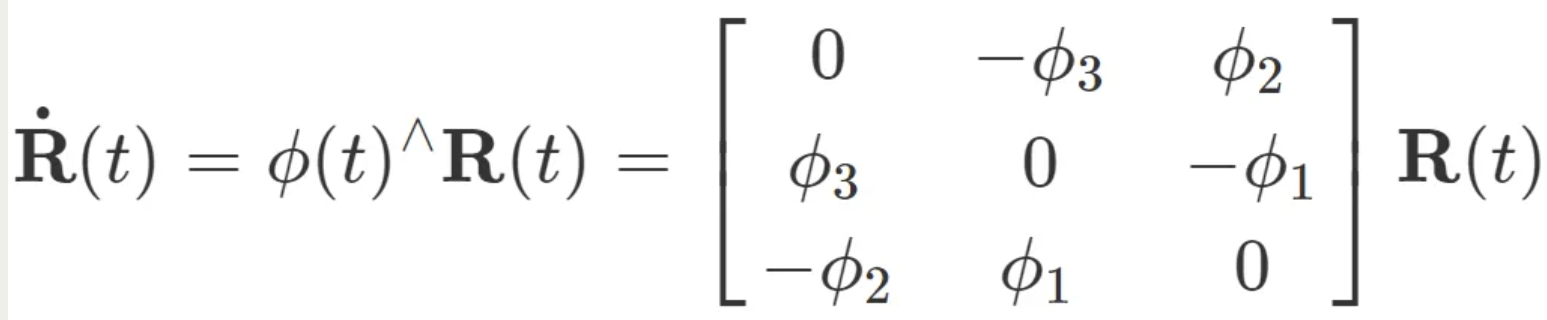
什么是反对称矩阵(skew symmetric matrix)
反对称矩阵其实是将三维向量和三维矩阵建立对应关系。它是这样定义的:如果一个3 X 3的矩阵A满足如下式子,那么A就是反对称矩阵。
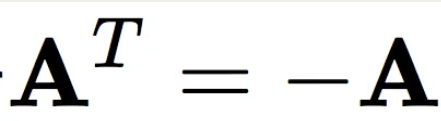
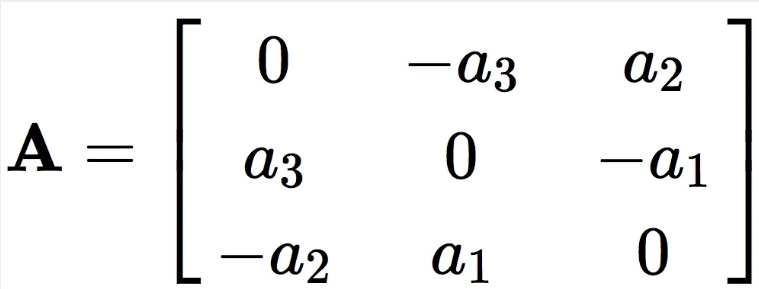
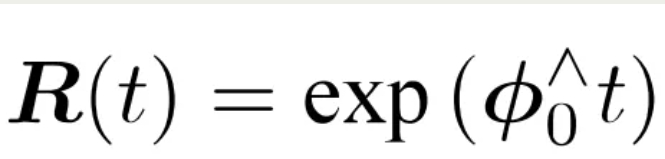
李代数小so(3)是三维向量φ的集合,每个向量φi的反对称矩阵都可以表达李群(大SO(3))上旋转矩阵R的导数,而R和φ是一个指数映射关系。也就是说,李群空间的任意一个旋转矩阵R都可以用李代数空间的一个向量的反对称矩阵指数来近似。
而李代数是由向量组成的,向量对加法运算是封闭的。
结合下面手写的笔记理解🙂
对极几何
用下图来直观的显示对极约束。表示的是一个运动的相机在两个不同位置的成像。
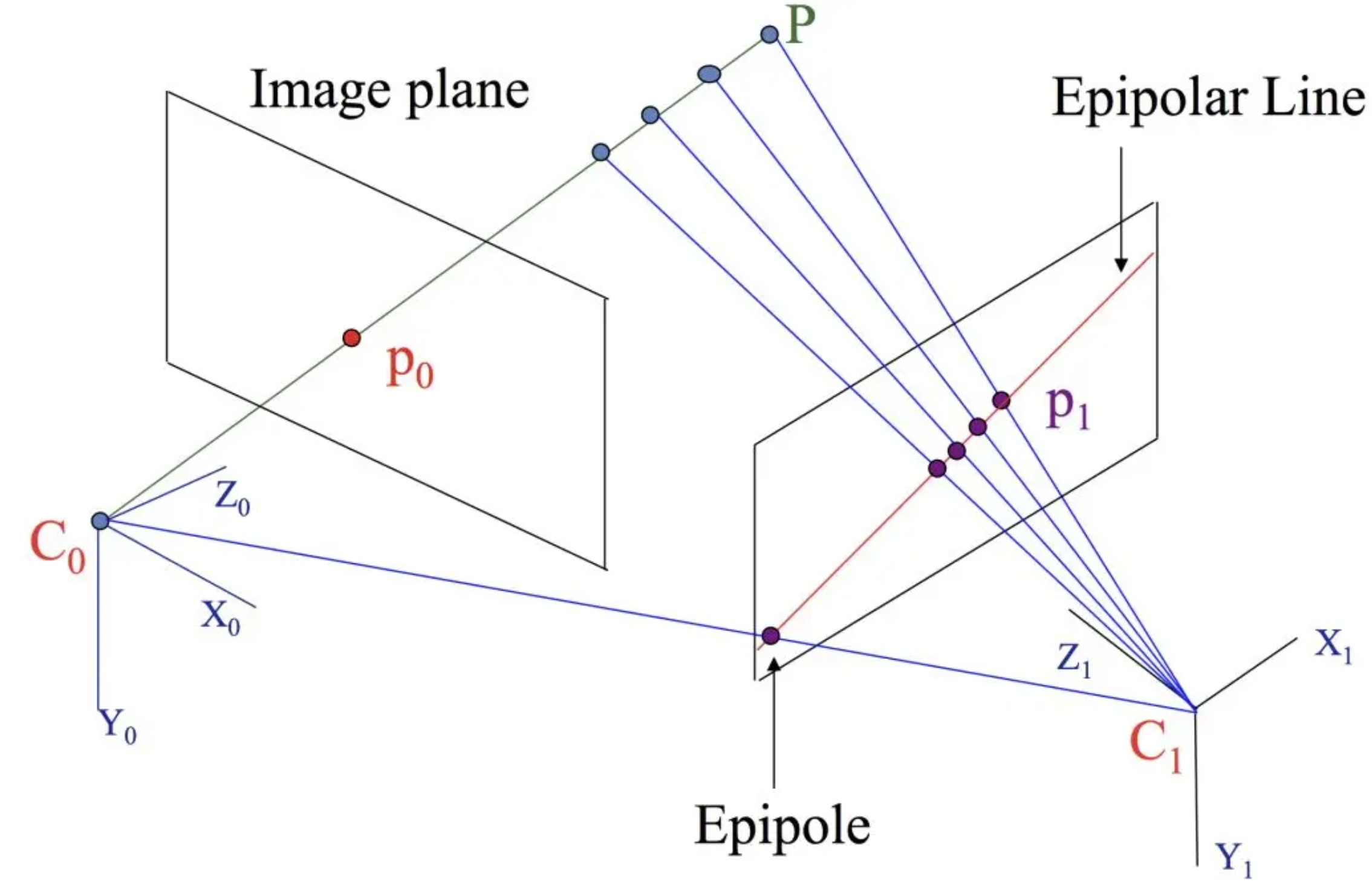
C0, C1分别是两个位置中相机的光心,也就是针孔相机模型中的针孔
P是空间中的一个三维点,p0, p1分别是P点在不同成像平面上对应的像素点
详细推导请展开
对于上图的左侧的图,如果将点P沿着C0-p0所在的直线移动,会发现P在左边相机的成像一直不变,都是p0,但是P在右边相机的成像点p1是一直在变化的。
C0-C1-P-p0-p1都是在同一个平面上的,可以想象C0-C1-P组成的平面是一个三角尺,它所在的平面称之为极平面(epipolar plane)。
其中和成像平面相交的直线称之为极线(epipolar line),两个光心C0, C1和成像平面的交点叫做极点(epipole)。
根据向量叉乘(是与向量 a, b都垂直的向量,其方向通过右手定则决定)以及向量的点乘(a·b=|a||b|cosθ),可以得到下面的公式:
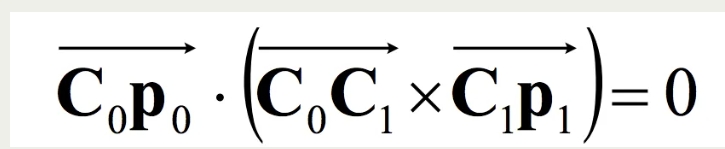
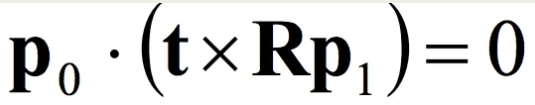
本质矩阵/本征矩阵(Essential Matrix)
把中间部分拿出来,记为下面的公式。也就是所谓的本质矩阵或本征矩阵(Essential Matrix)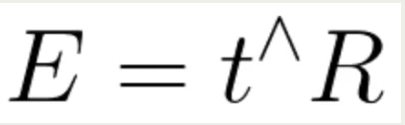
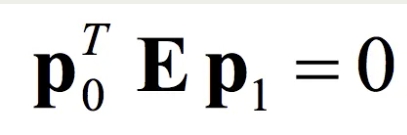
基础矩阵(Fundamental Matrix)
对于上面对极几何的本质矩阵(Essential Matrix)加上相机内参K,就可以得到基础矩阵(Fundamental Matrix)。
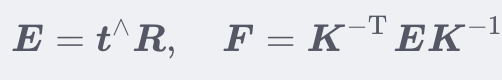
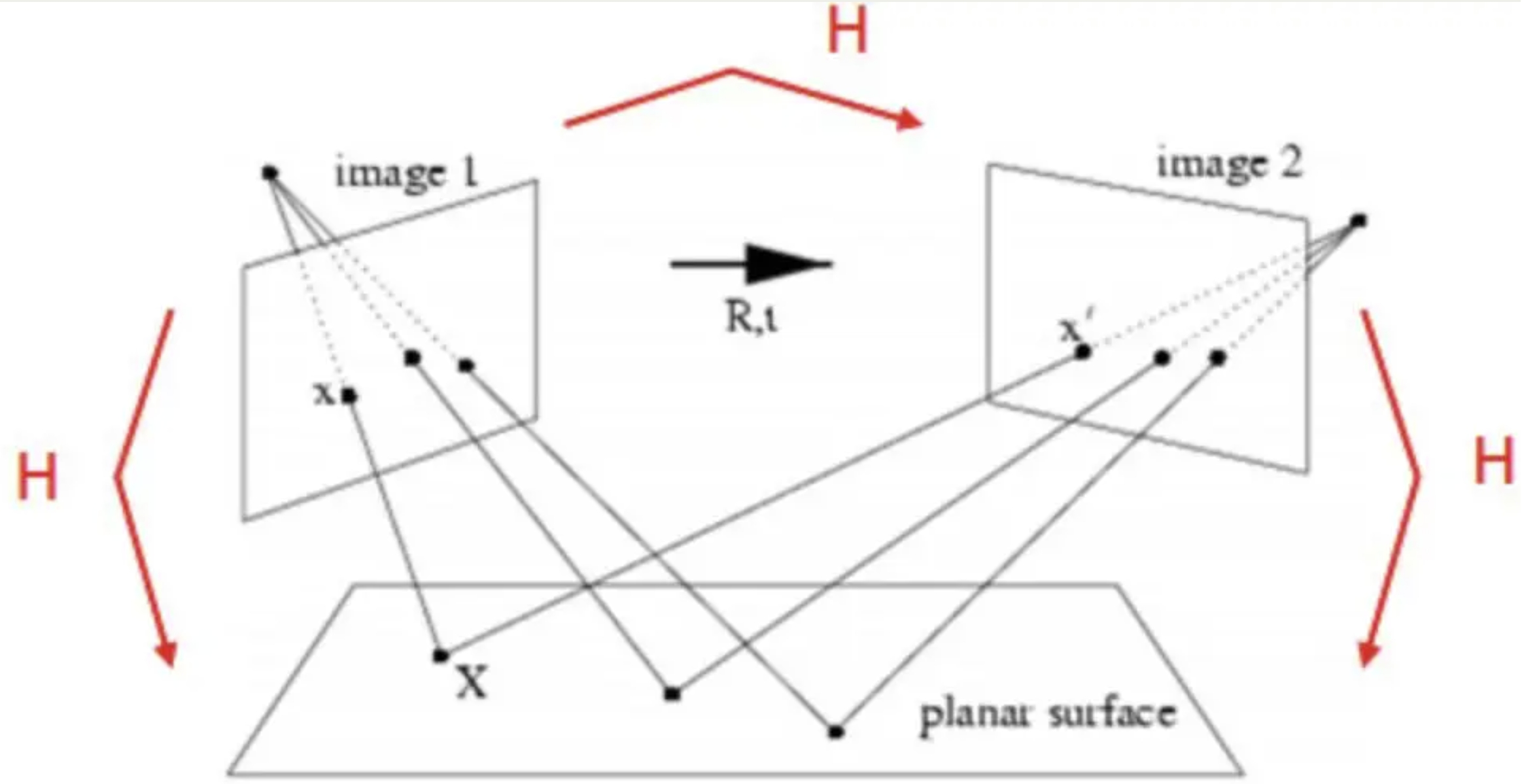
单应矩阵(homography matrix)
单应矩阵描述的就是:同一个平面的点在不同图像之间的映射关系。
详情请展开
如下图所示,两个不同的相机拍摄同一个平面。

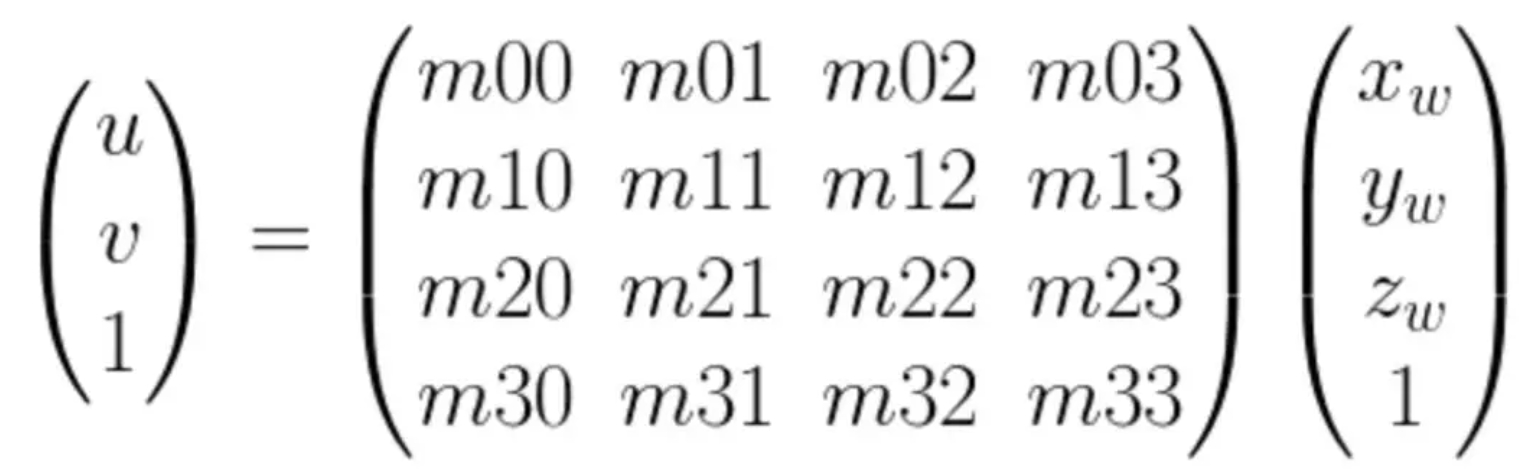
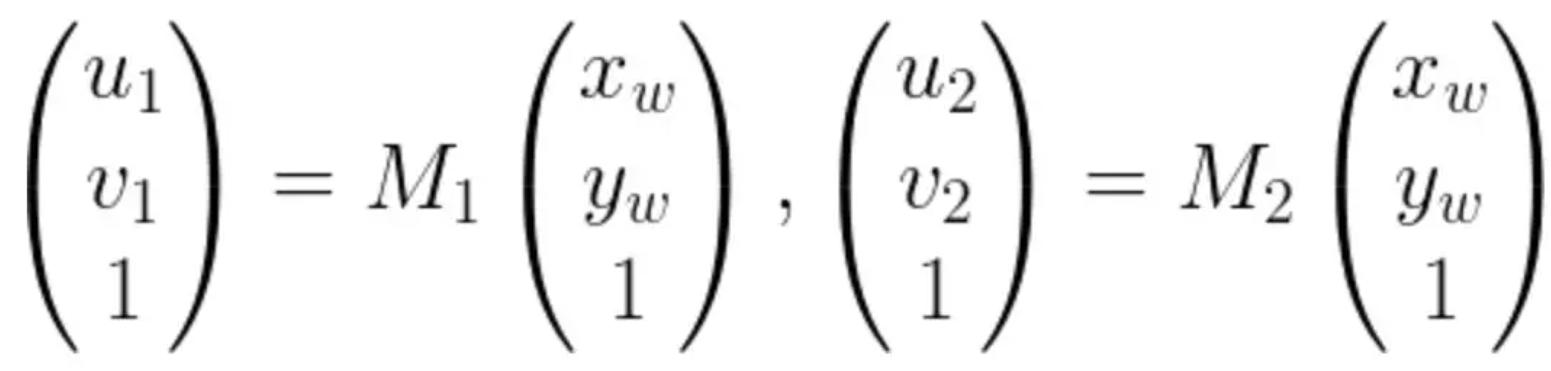
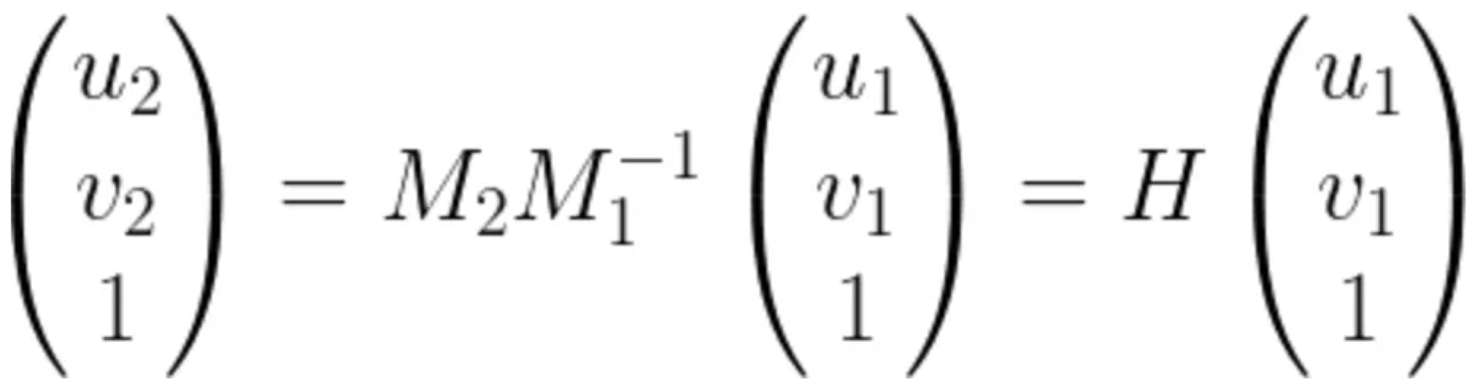
非线性优化
SLAM中的最小二乘问题
见下图。一般在视觉SLAM中后端优化就是约束项大于未知数的个数(超定问题),采用最小二乘问题求解。
(m为约束项也就是方程数,n为未知数)


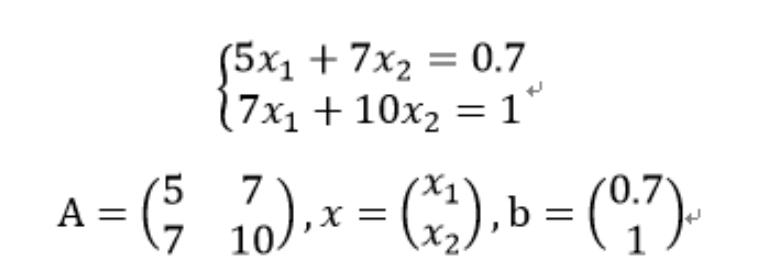
什么是雅可比矩阵
雅可比矩阵就是一阶偏导数矩阵。
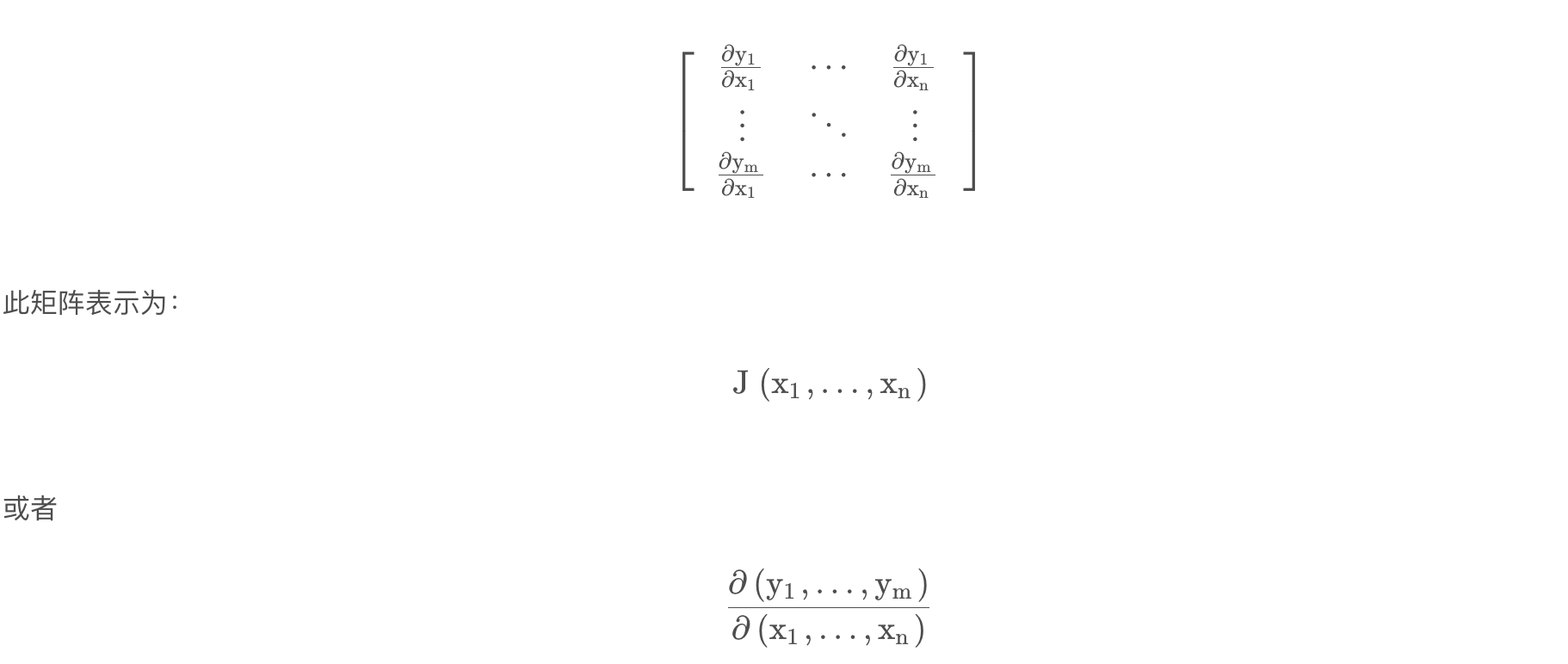
什么是Hessian矩阵
海森矩阵(Hessian matrix 或 Hessian)是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵。对于下面函数有:

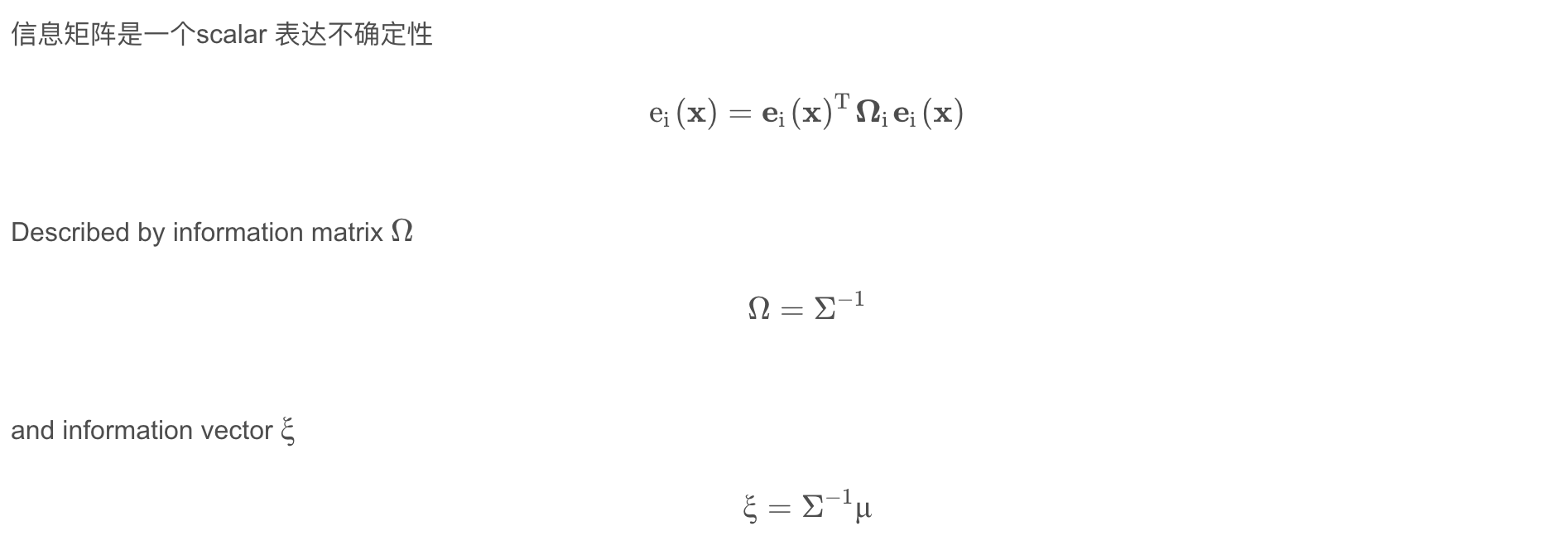
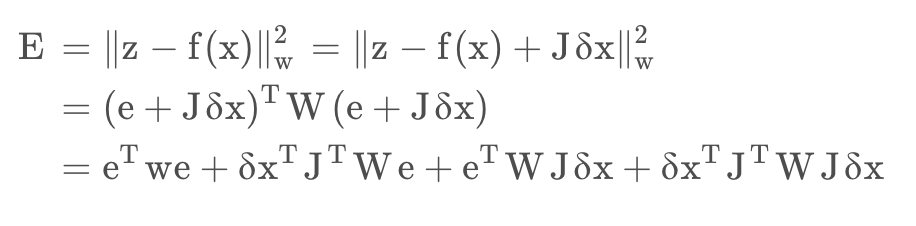
矩阵分解
展开详细解读矩阵分解~
矩阵分解就是分解成正交矩阵、对角矩阵、三角矩阵,矩阵分解的几何意义就是把一个线性变换分解开来,分别是缩放,切边和旋转。矩阵因子的作用就是要把缩放,切边和旋转分解出来理解一个矩阵的作用。
矩阵分解中常用矩阵
矩阵分解中常用矩阵
正交矩阵
如果一个矩阵和它的转置矩阵的乘积为单位矩阵, 那么这个矩阵就是正交矩阵。为什么叫正交矩阵?把正交矩阵写成向量的形式, 那么这些向量除了自己和自己的点积为1,其他任意两个不同向量之间的点积全部为0.而向量点积为0的情况叫正交。 正交矩阵其实就可以理解成一组基,也就是坐标系。因此矩阵分解中都希望直接转换成正交矩阵相乘的形式。
PS:正交矩阵,并不改变物体的形状,但是进行了旋转。
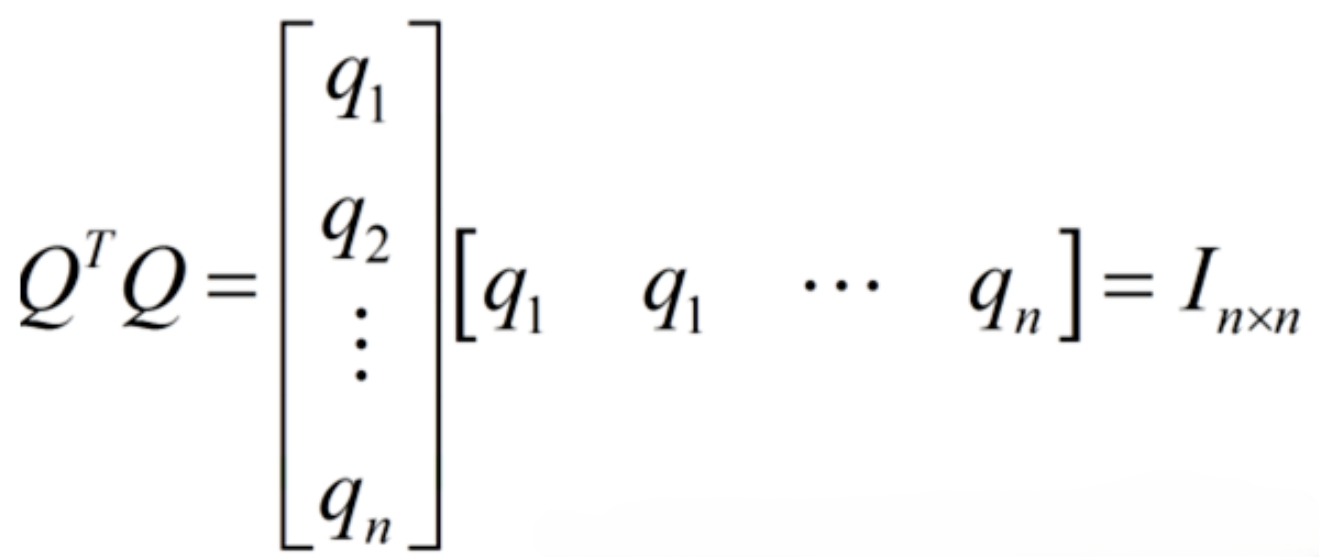
对角矩阵
乘以一个对角矩阵,好比对每个坐标轴进行缩放,包括方向,和压缩。正数的乘法:正数好比在原方向上的缩放, 大于1,表示伸长,小于1,表示缩小。负数的乘法:负数表示反反向。零的乘法:零表示空间压缩。
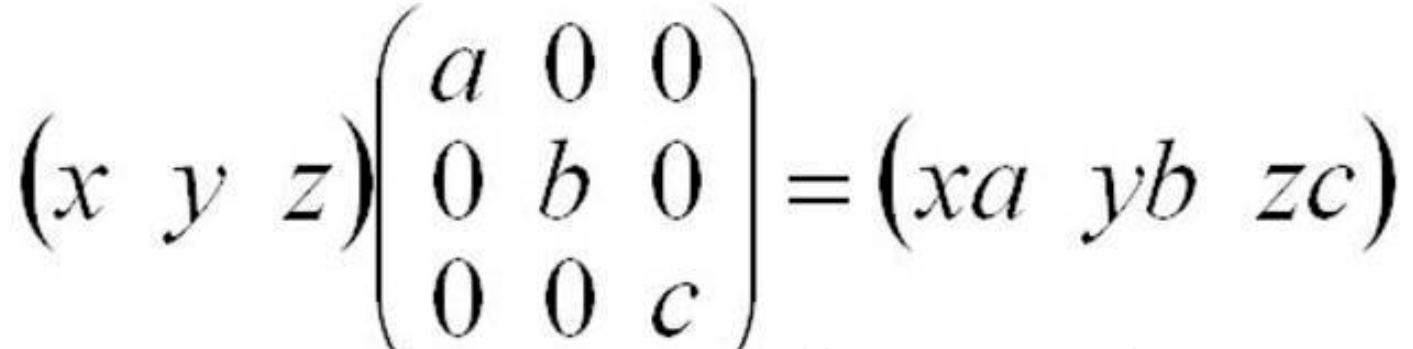
三角矩阵
分为上三角矩阵与下三角矩阵。上三角矩阵的作用好比进行右上的切变,水平的斜拉。下三角矩阵:同样是切边,不过是往左下切边,垂直方向的下拉。直观理解请见下图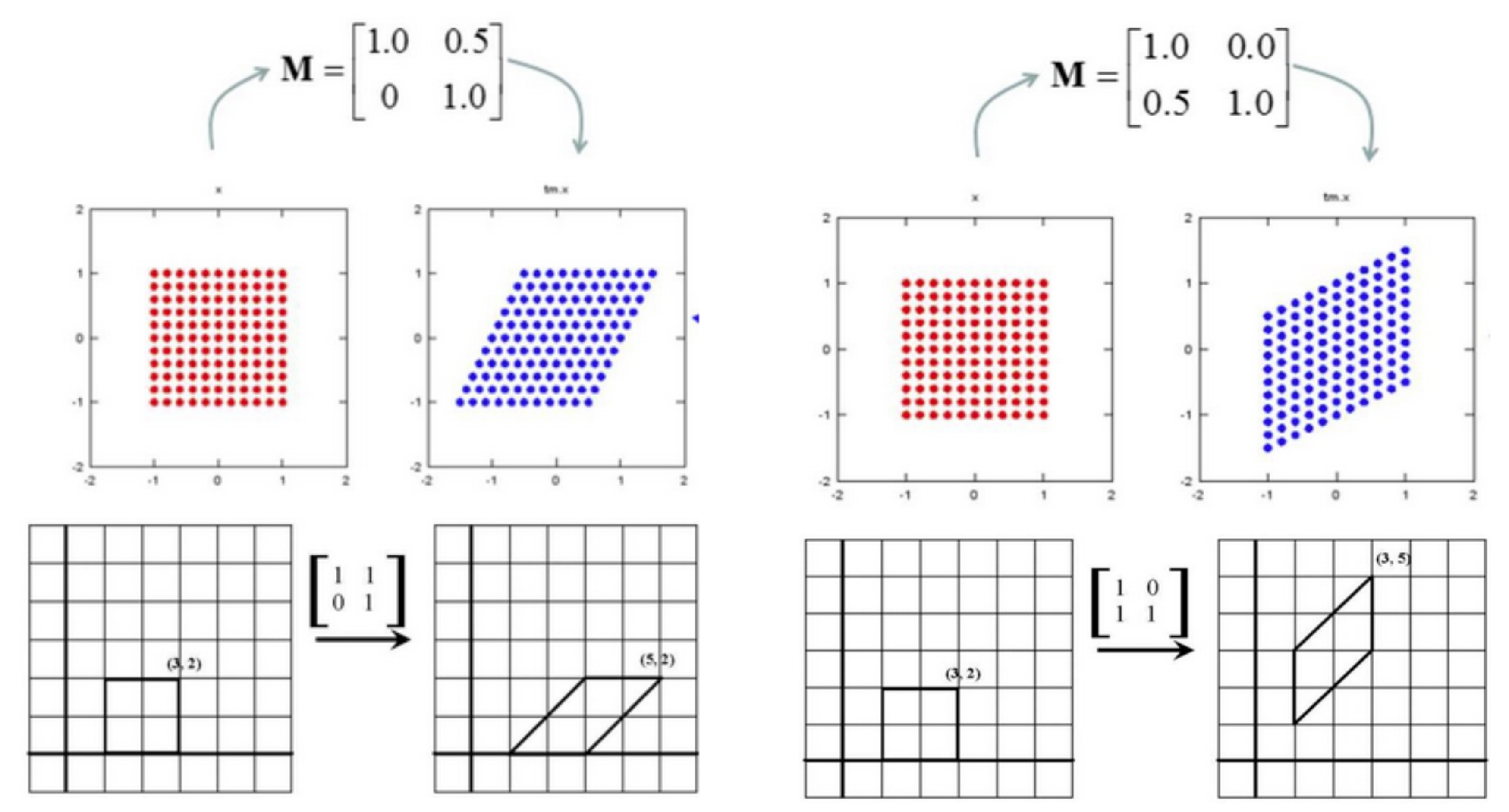
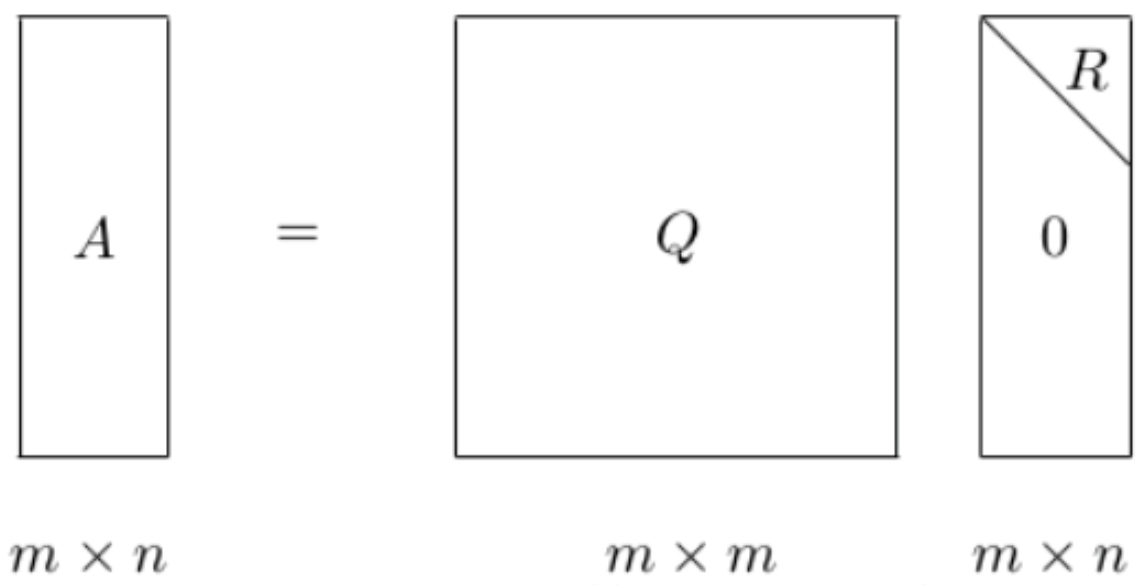
QR分解
当A是非奇异的实矩阵,实矩阵A能够表示成一个正交矩阵Q(QTQ=I)与上三角矩阵R的积,A=Q*R称为A的QR分解。如下图所示:
LDLT分解
对称矩阵A可以分解成一个下三角矩阵L(Lower下)和一个对角矩阵D(Diagonal对角线)以及一个下三角矩阵L的转置LT三个矩阵相乘的形式。如下式
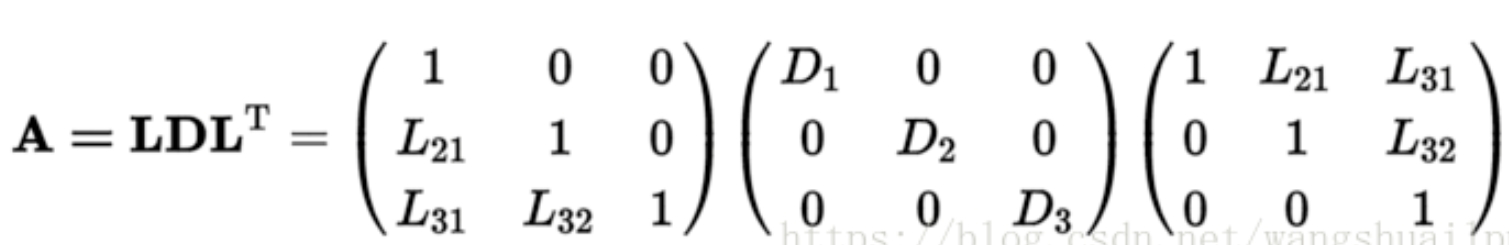
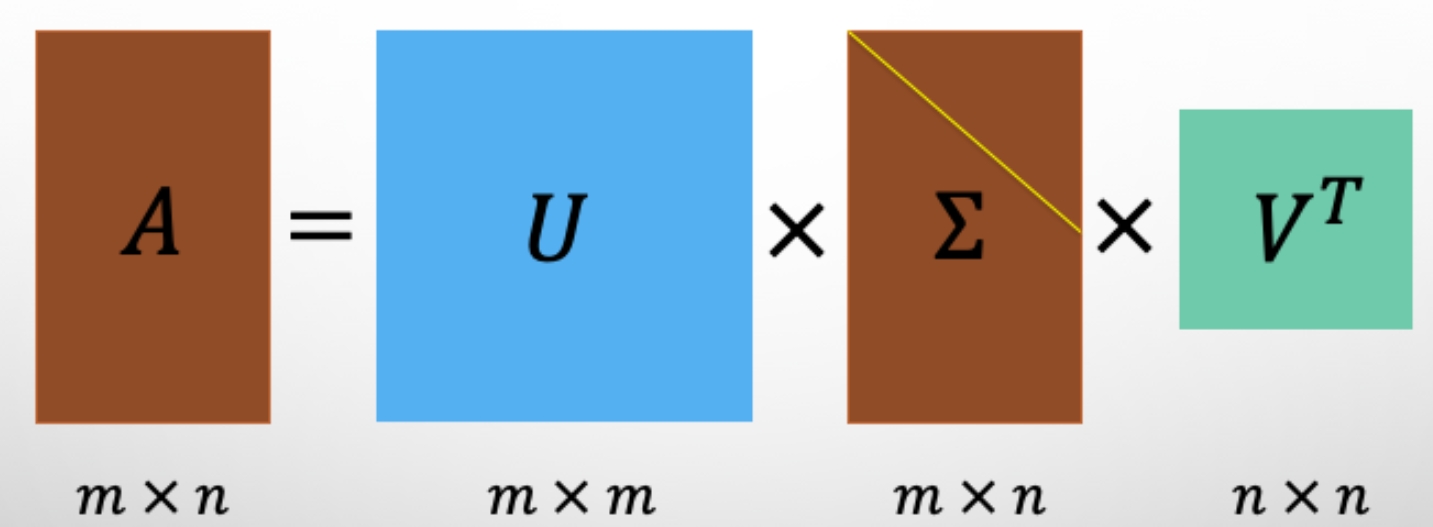
SVD分解
矩阵的奇异值分解(SVD)在最优化问题、特征值问题、最小二乘问题及广义逆问题中有巨大作用,奇异值分解将QR分解推广到任意的实矩阵,不要求矩阵式可逆,也不要求是方阵。奇异值和特征值相似的重要意义,都是为了提取出矩阵的主要特征。假设A是一个m∗n阶矩阵,如此则存在一个分解m阶正交矩阵U、非负对角阵Σ和n阶正交矩阵V使得下式满足:
SVD解决了特征值分解中只能针对方阵而没法对更一般矩阵进行分解的问题。
(QR分解要求A是非奇异的实矩阵,LDLT分解要求矩阵A是对称矩阵)
奇异值有个突出的性质:在大部分情况下,当把矩阵Σ里的奇异值按从大到小的顺序排列以后,就会发现,奇异值σ减小的速度特别快。在很多时候,前10%甚至前1%的奇异值的和就占了全部奇异值和的99%以上。换句话说,大部分奇异值都很小,基本没什么用。既然这样,那我们就可以用前面r个奇异值来对这个矩阵做近似。因此上面的矩阵问题就可以转化为一个低秩矩阵的问题。
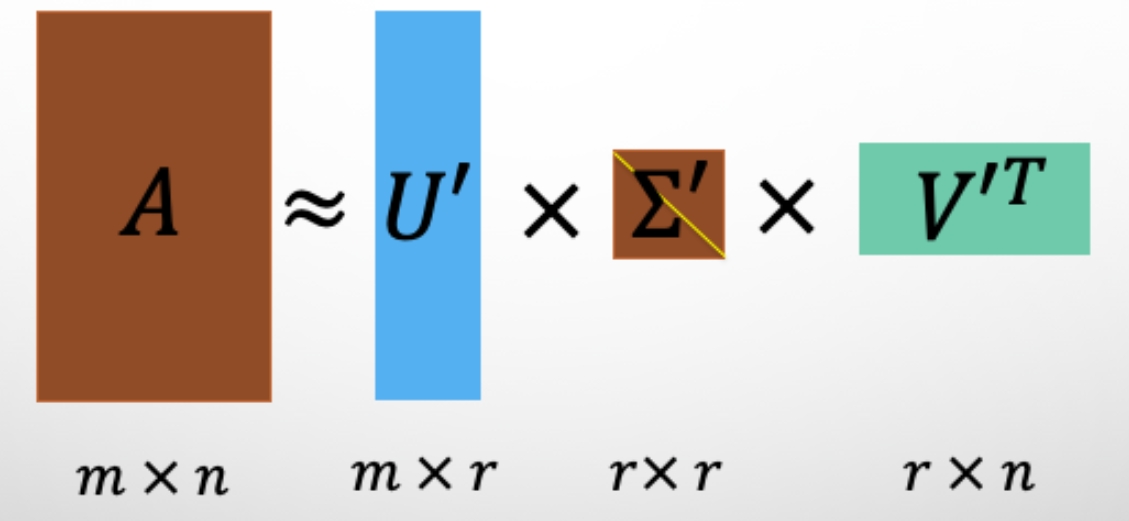
Ax=0的解为最小奇异值对应的向量
SLAM中三角化地图点,PnP等一些问题都是求解超定方程Ax=0(此处的A就是最小二乘法中的A)A是 m*n的矩阵,且m>n。 而这个方程的非零解就是ATA的最小特征值和对应的特征向量. 至于原因,推导过程稍微有点参考资料 1, 2图优化(Graph-based Optimization)
SLAM的后端一般分为两种处理方法,一种是以扩展卡尔曼滤波(EKF)为代表的滤波方法,一种是以图优化为代表的非线性优化方法。
在计算资源受限、待估计量比较简单的情况下,EKF为代表的滤波方法比较有效,经常用在激光SLAM中。但是它的一个大缺点就是存储量和状态量是平方增长关系,因为存储的是协方差矩阵,因此不适合大型场景。
在发现了BA是稀疏的后,其计算就可以加速了,因此图优化就成为了SLAM的主流方法。
图优化里的图就是数据结构里的图,一个图由若干个顶点(vertex),以及连接这些顶点的边(edge)组成。在SLAM中,顶点一般表示机器人的位姿或者地图中的特征点,边一般表示两个顶点之间的约束关系。
Bundle Adjustment(BA)
Bundle Adjustment(BA)中文有多种翻译法:光束法平叉、束调整、捆集调整、捆绑调整等。BA的本质是一个优化模型,其目的是最小化重投影误差(Re-projection Error)。 而通常使用的是窗口BA,它将当前图像和之前的n-1幅图像帧作为一个窗口进行优化,这样不仅可以跟踪前一个相机位姿还可以跟踪更之前的相机位姿,保证当前和前n-1个相机位姿一致。因此,窗口BA可以减小漂移。窗口大小n的选择决定了计算复杂度,选择较小的窗口数量可以限制优化的参数的数量,使得实时BA成为可能。

SLAM中的各种地图表达方式
SLAM中的地图表示方式有很多种,主要包括拓扑地图、几何地图、语义地图、特征地图等。下面将分别介绍这几种地图。
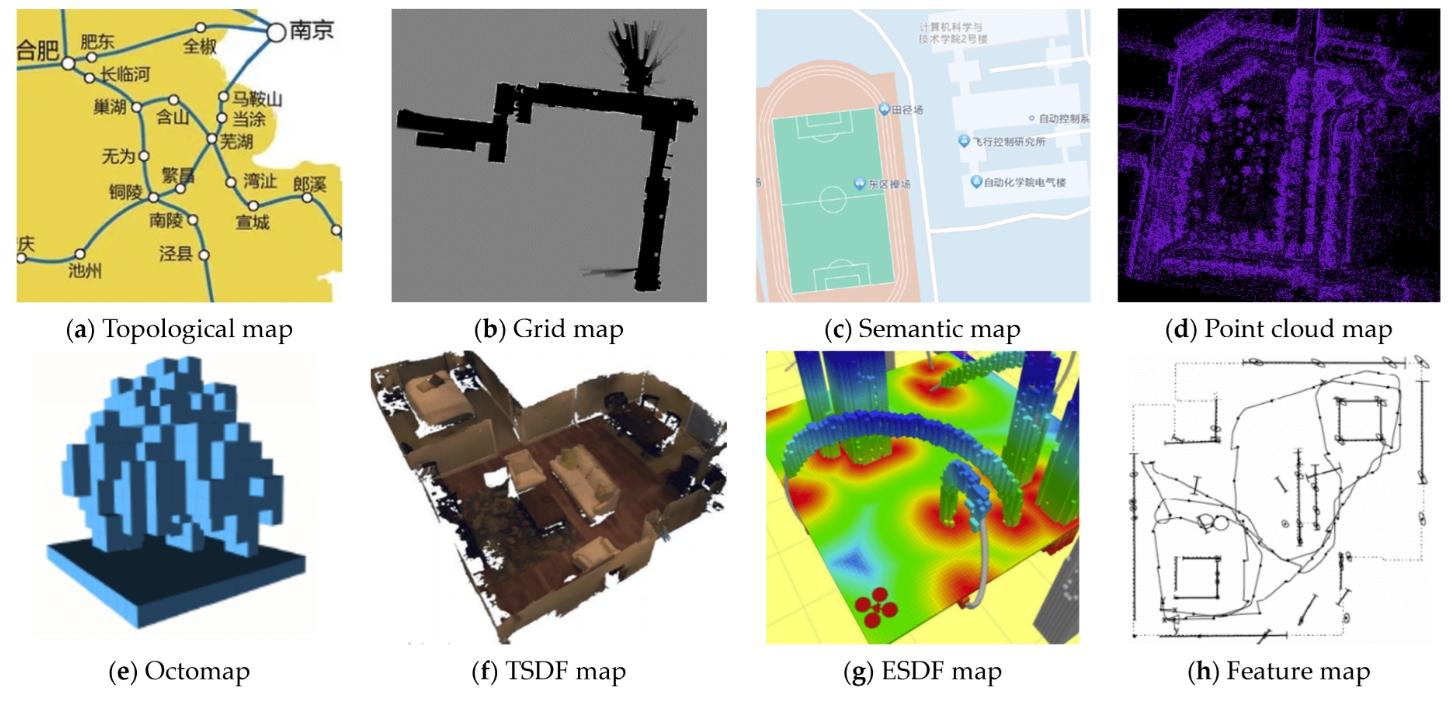
关于各种地图的表征形式请展开查看
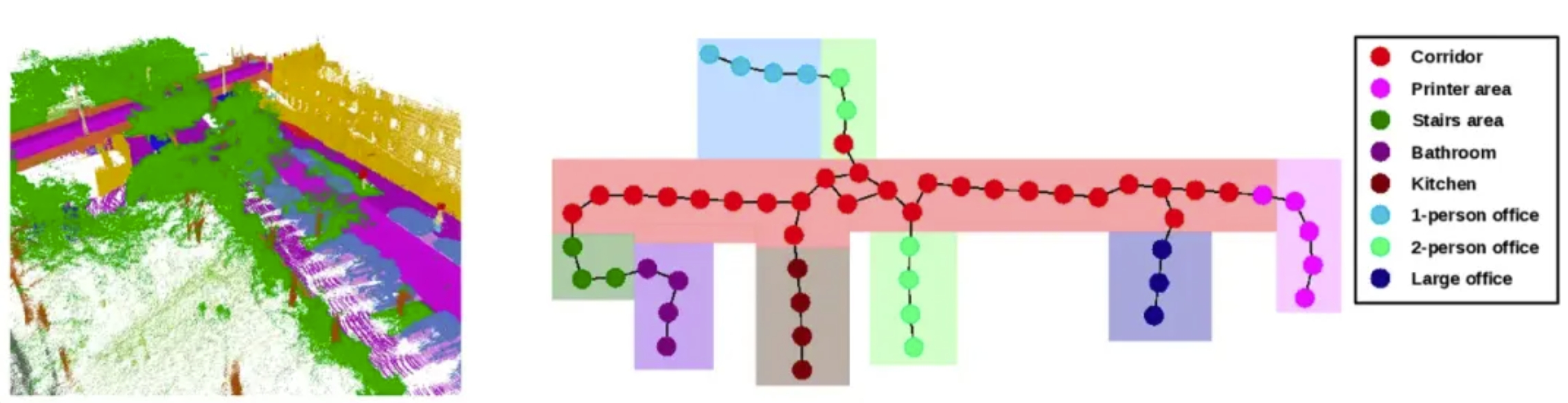
拓扑地图(Topological Map)
拓扑地图使用节点和边来表示环境,其中节点表示重要位置(如拐角、门口),边表示这些位置之间的可达路径。拓扑地图注重表示环境的连接关系,而不是具体的几何细节。这种地图表示方法适用于大型、复杂环境中的高效路径规划和导航。
几何地图(Geometric Map)
度量地图(Metric Map)或几何地图(Geometric Map)是SLAM种较为常用的一种表示方法,常见的点云(PointCloud)、八叉树地图(OctoMap)、栅格地图(Grid Map)等都属于度量地图。
而根据地图的稠密程度,还可进一步分为:稀疏地图、稠密地图。
根据地图是连续的还是离散的,还可进一步分为:离散地图、连续地图。栅格地图、体素地图(Voxel Map)就是典型的离散地图,把空间进行了划分,然后离散化表达;连续地图是采用高斯过程或者NeRF方式建立的地图。
特征地图(Feature Map)
特征地图(Feature Map)是仅保留特征的地图,常见于视觉SLAM。一些场景,例如水下的定位放置一些标志物,这样建立的地图就是特征点地图。视觉SLAM一般提取特征点匹配后建立特征点地图。除了点特征意外,线特征和面特征也可以建立地图,但也属于是特征地图的一种。

点云地图(Point Cloud Map)
点云地图(Point Cloud Map)是利用点云形式表示地图,常见的激光雷达SLAM建立的都是点云地图。

面元(Surfel)

深度图(Depth Map)
三角网格(Mesh)
点云是一个个离散的空间点,虽然远看能看出物体的轮廓,但是拉近了看是一个个分散的空间点。分辨率比较低,也没办法进行三维打印,点云网格化就是用点云生成网格,最后得到的是一个连续(相对于前面的离散点)的表面。
我们常说的mesh或者ImMesh中的mesh,就是三角网格。三角网格是由一系列的三角形组成的,每个三角形由三个顶点组成。三角网格是一种常见的三维模型表示方法,可以用来表示物体的表面。
当然也有四角网格。如下图所示。
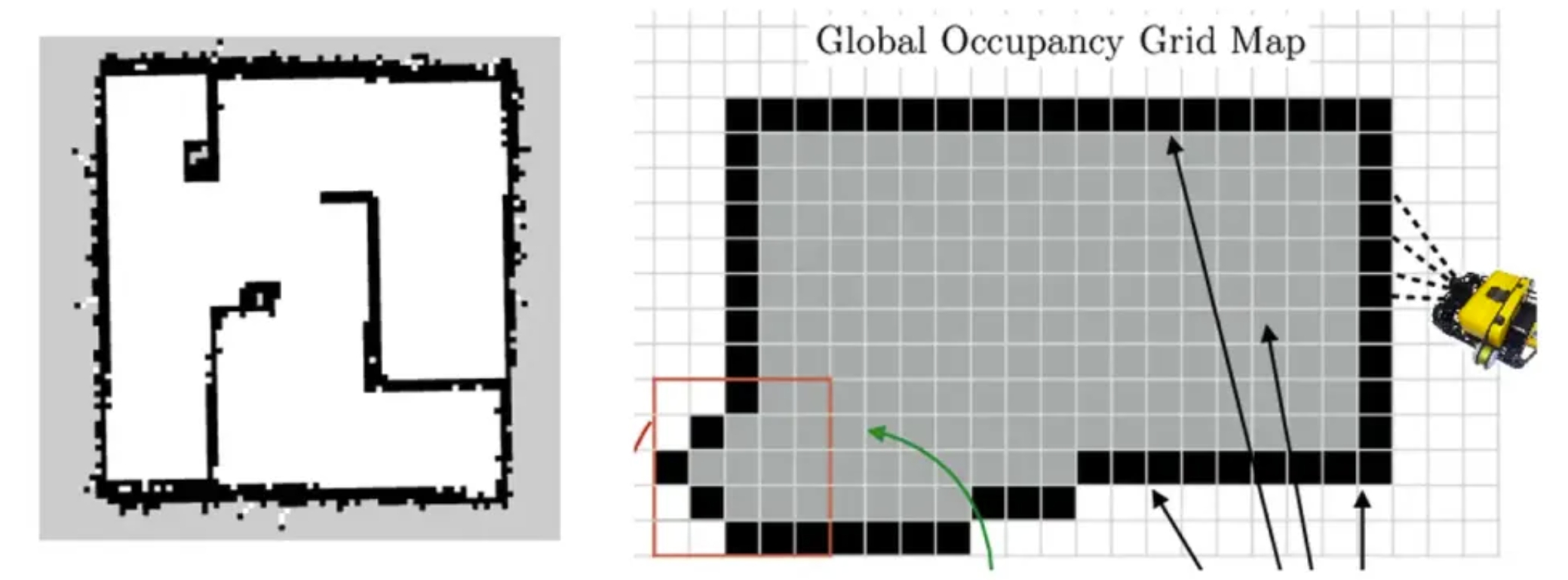
栅格地图(Grid Map)
栅格地图(Grid Map)将空间划分为均匀的网格,每个网格存储一个值,表征地图的属性。一种常见的方式,用三种状态:占用、空闲、未知,表示某个栅格是否被占用,这种表达方式称作“占用栅格地图”(Occupancy Grid Map),机器人导航常用栅格地图,在“空闲”栅格中规划运动轨迹。一般来说,栅格地图指的是二维平面地图。
体素地图(Voxel Map)
体素地图(Voxel Map)可以理解为三维的栅格地图,当然也包括占用体素地图(Occupancy Grid Map)。如果是无人机这类的导航,一般需要用到3D的栅格地图。和点云地图相比,体素地图的“分辨率”更低,对点云地图进行了离散化。
SDF
TSDF
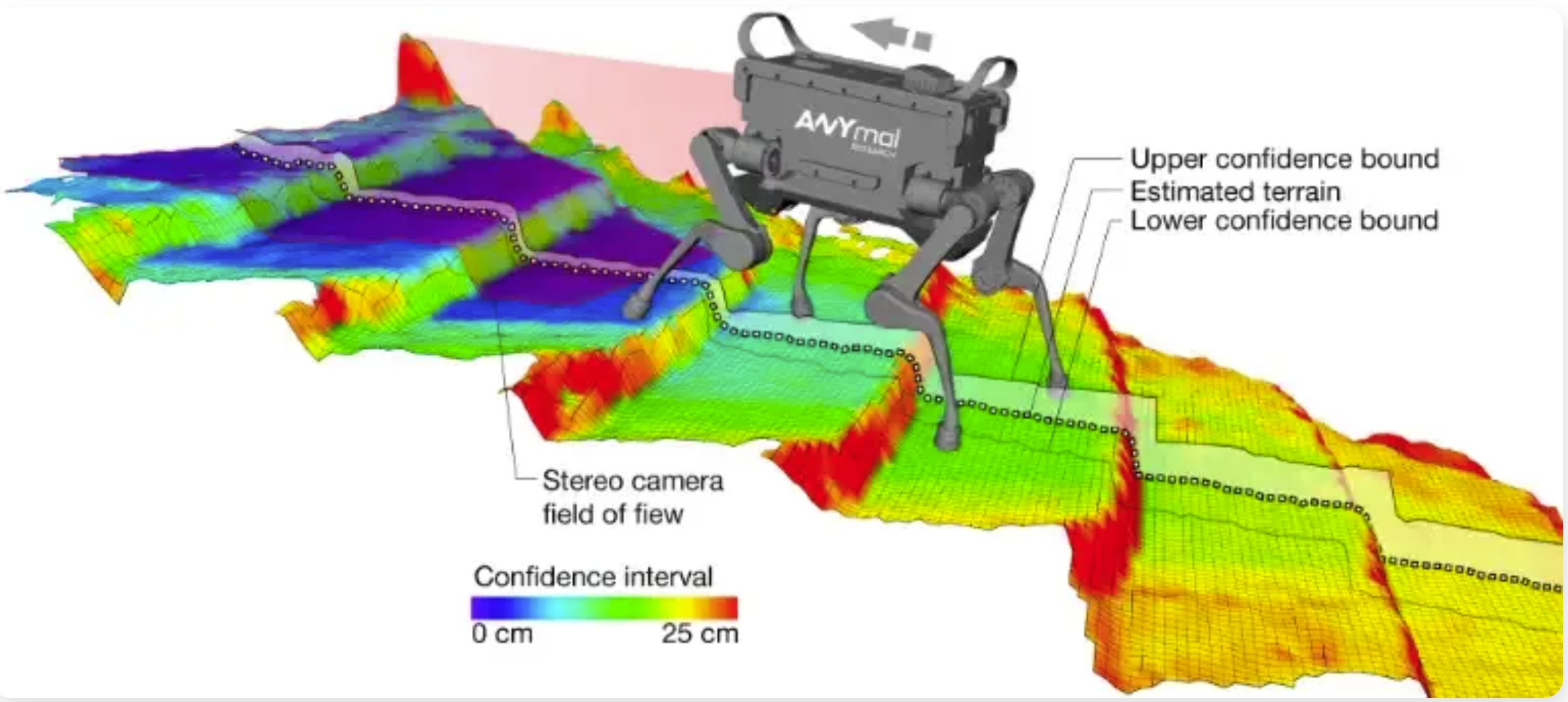
高程地图(Elevation Map)
高程地图(Elevation Map)也称2.5D地图。如果是平坦地面、二维场景,用栅格地图就可以;如果是无人机,需要用到三维场景体素地图;但如果是无人车在非平坦路面运行、或者是四足/轮式机器人在野外的行进,需要对地形进行建模,常用的方式就是高程地图。在栅格地图的基础上增加了一个维度即高度。
神经辐射场地图(Neural Radiance Fields, NeRF)
神经辐射场地图(Neural Radiance Fields, NeRF)是一种新兴的三维场景表示和渲染技术,通过神经网络隐式地表示三维空间中的颜色和密度场。 更多关于NeRF的介绍,请见博客Link.
高斯球(3D Gaussian Splatting)
3DGS也是一种新兴的三维场景表示和渲染技术,通过高斯球来代表三维结构。除了3DGS以外,还有2DGS,4DGS等等。 更多关于3DGS的介绍,请见博客Link.
语义地图(Semantic Map)
语义地图(Semantic Map)是包含了语义信息的地图,语义信息可以是物体的种类、姿态和形状等描述。例如,无人驾驶需要知道地图中那些是车道、哪些是障碍。只要包含于语义信息就可以算是语义地图。

SLAM系列demo展示
展开查看
开源代码
Visual SLAM系列代码改进与解读
Learning-based VO系列代码改进与解读
3DGS-SLAM系列代码改进与解读
LiDAR-SLAM系列代码改进与解读
LOAM系列算法的解读与复现demo请见博客Link.
Event-based SLAM系列代码改进与解读
LiFi-based SLAM
LiFi-based SLAM是一种基于可见光通信的SLAM技术,通过可见光通信实现定位和建图。LiFi-based SLAM的优势在于它不受电磁干扰,安全性高,且可以实现高精度的定位。LiFi-based SLAM的应用场景包括室内定位、导航、Localization-based Services等。