贪心算法(greedy algorithm)基本思想是在问题的每个决策阶段,都选择当前看起来最优的选择,即贪心地做出局部最优的决策,以期获得全局最优解。
贪心思路的本质,如果找不到重复计算,那就通过问题中一些隐藏较深的规律,来减少冗余计算。
从局部最优推导出全局最优,但是有时局部最优并不一定能导出全局最优(比如背包问题)
而贪心算法的关键点是:无套路。因此本博文仅仅是总结一些贪心算法相关的例题。
实际做题时,需要根据题目的特点,来判断是否适合使用贪心算法。可从下面三个方向思考:
贪心算法与动态规划区别:零钱兑换(背包问题)
相同点在于都是解决优化问题的,也依赖最优子结构的性质。但是工作原理不一样~。
- 动态规划会根据之前阶段的所有决策来考虑当前决策,并使用过去子问题的解来构建当前子问题的解。
- 贪心算法不会考虑过去的决策,而是一路向前地进行贪心选择,不断缩小问题范围,直至问题被解决。

贪心算法的解法。在此代码中,假设最小面值为min,那么时间复杂度应该是O(amount/min)比起背包问题的动态规划解法时间复杂度O(n*amount)少不小。但是对于某些硬币面值组合,贪心算法并不能找到最优解(在leeetcode上测试并无法通过所有的样例)因此,贪心算法并不能用于解决背包问题,背包问题只能用动态规划去解决~。
用完全背包问题思路的动态规划解法~
一维动态规划解法
因此,对于零钱兑换问题,贪心算法无法保证找到全局最优解。它更适合用动态规划解决。
一般情况下,贪心算法的于以下两种。
- 可以保证找到最优解:贪心算法在这种情况下往往是最优选择,因为它往往比回溯、动态规划更高效。
- 可以找到近似最优解:贪心算法在这种情况下也是可用的。对于很多复杂问题来说,寻找全局最优解非常困难,能以较高效率找到次优解也是非常不错的。
- 贪心选择性质:一个问题的整体最优解可以通过一系列局部最优的选择,即贪心选择来达到。只有当局部最优选择始终可以导致全局最优解时,贪心算法才能保证得到最优解。
- 最优子结构性质:原问题的最优解包含子问题的最优解。
分数背包问题
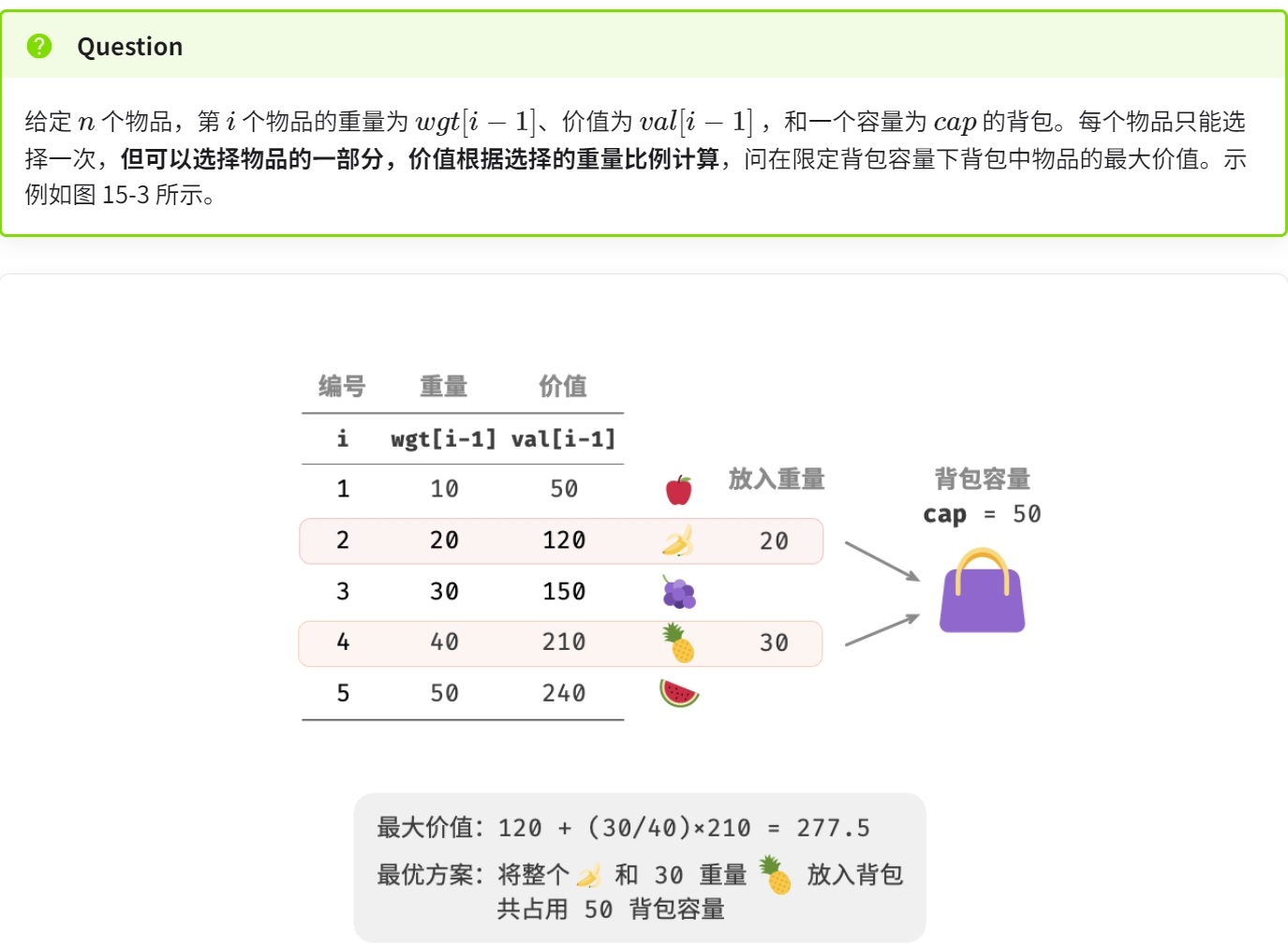
此题跟 0-1 背包问题整体上非常相似,状态包含当前物品和容量,目标是求限定背包容量下的最大价值。
不同点在于,本题允许只选择物品的一部分。我们可以对物品任意地进行切分,并按照重量比例来计算相应价值。
如下图所示。
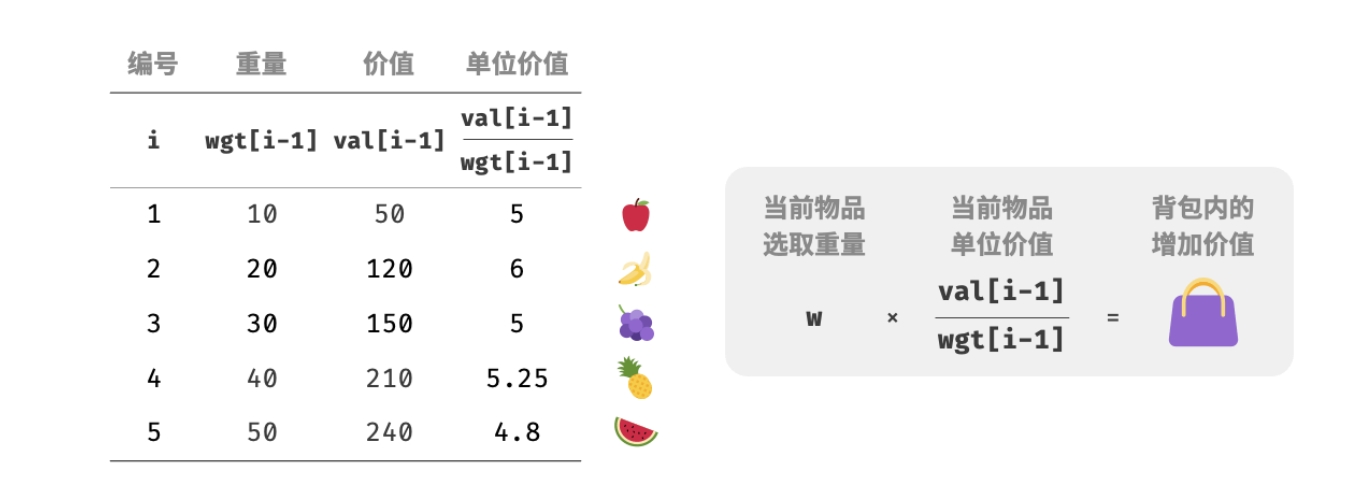
1.将物品按照单位价值从高到低进行排序。
2.遍历所有物品,每轮贪心地选择单位价值最高的物品。
3.若剩余背包容量不足,则使用当前物品的一部分填满背包。
Click to expand the code。时间与空间的复杂度都为O(N)
最大容量问题
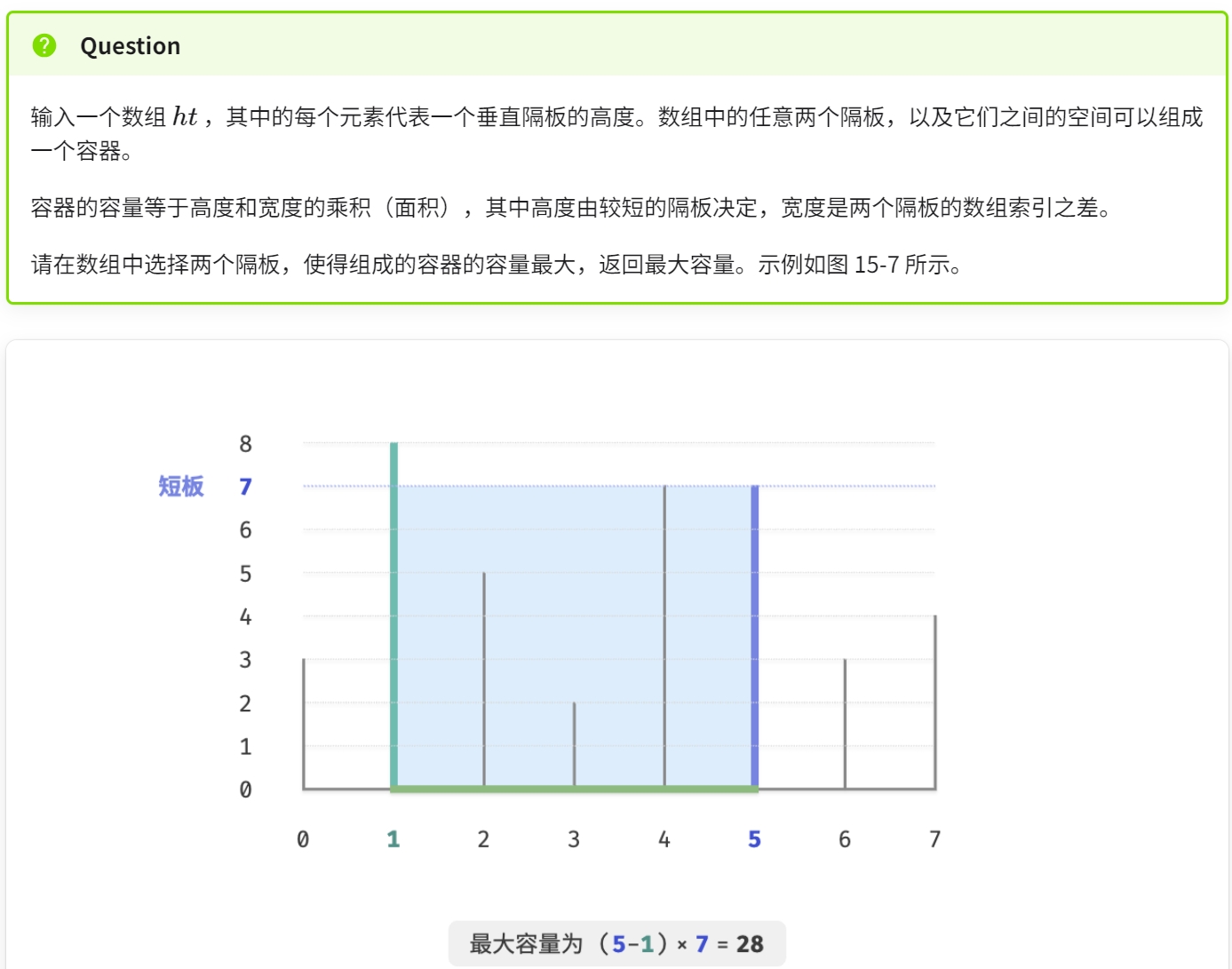
Click to expand the code.时间复杂度为O(N),空间复杂度为O(1)。贪心算法比穷举更快,是因为每轮的贪心选择都会“跳过”一些状态。从而导致一些状态无法被验证。但是通过代码分析可以发现跳过的这些状态都必然不是最优解,故此跳过他们可以加速同时不影响最终结果
分发饼干

Click to expand the code,时间复杂度为O(nlogn),空间复杂度为O(1)
既可动态规划,又可贪心算法
根据这类题目的分析,可以发现,其实不少贪心算法都可以用动态规划算法Link解决。当然动态规划算法是成套路的。而贪心算法则是可以更快的解题。同时也可以通过部分的测试案例(最佳的情况,或者说符合贪心算法标准就是通过100%)
摆动序列

Click to expand the code(动态规划解法)
Click to expand the code。贪心算法直接统计每次结果,从局部的值推导全局值
最大子数组和

Click to expand the code。动态规划解法。时间复杂度为O(N),空间复杂度为O(N)
Click to expand the code。贪心算法的解法,当前“连续和”为负数的时候立刻放弃,从下一个元素重新计算“连续和”,因为负数加上下一个元素 “连续和”只会越来越小。时间复杂度为O(N),空间复杂度为O(1)
K次取反后最大化的数组和

Click to expand the code.时间复杂度为O(Nlogn),空间复杂度为O(1)
加油站

Click to expand the code。局部最优:当前累加rest[i]的和curSum一旦小于0,起始位置至少要是i+1,因为从i之前开始一定不行。全局最优:找到可以跑一圈的起始位置。(注意题目说了如果有解,必然是唯一解)
柠檬水找零

Click to expand the code,模拟算法计数器。时间复杂度为O(N),空间复杂度为O(1).但这其实也是算贪心算法!!!
局部最优:遇到账单20,优先消耗美元10,完成本次找零。全局最优:完成全部账单的找零。
局部最优可以推出全局最优,因为每次找零都是最优的,那么最终的找零也是最优的。
两次贪心策略:分发糖果

Click to expand the code,时间与空间复杂度O(N)。
确定一边之后,再确定另一边,例如比较每一个孩子的左边,然后再比较右边,如果两边一起考虑一定会顾此失彼。
先确定右边评分大于左边的情况(也就是从左向右遍历)此时局部最优:只要右边评分比左边大,右边的孩子就多一个糖果,全局最优:相邻的孩子中,评分高的右孩子获得比左边孩子更多的糖果。(局部最优可以推出全局最优)
再确定左孩子大于右孩子的情况(也就是从右向左遍历)
特殊情况:某个值既大于它的左边,又大于它的右边。也就是candyVec[i]只有取最大的才能既保持对左边candyVec[i - 1]的糖果多,也比右边candyVec[i + 1]的糖果多。
根据身高重建队列

Click to expand the code.遇到两个维度权衡的时候,一定要先确定一个维度,再确定另一个维度。但是题目关键应该还是如何确定排序的方法,要先按什么排序,再按什么排序!
空间复杂度为O(N),时间复杂度为O(N2)因为用了vector的insert操作,为此时间复杂度并不是O(N)。sort的时间复杂度为O(NlogN)。

判断区间重叠
跳跃游戏
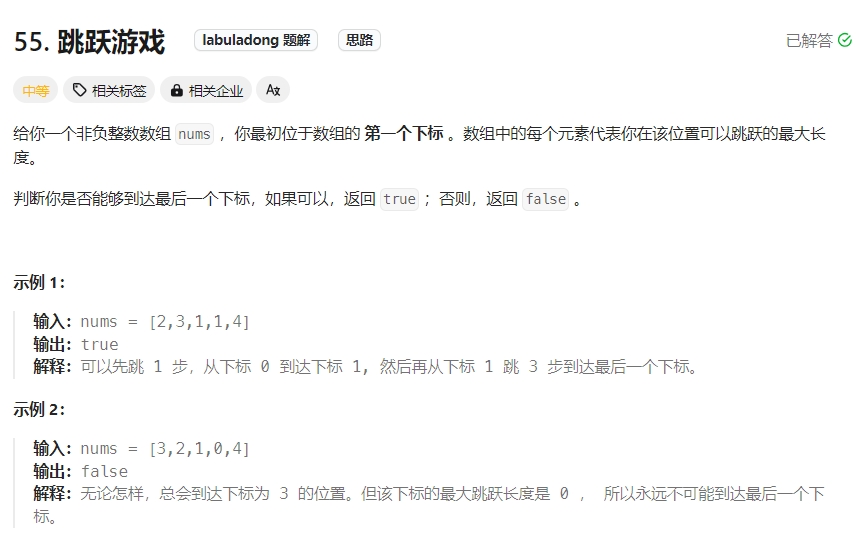
Click to expand the code(问题就转化为跳跃覆盖范围究竟可不可以覆盖到终点!)贪心算法局部最优解:每次取最大跳跃步数(取最大覆盖范围),整体最优解:最后得到整体最大覆盖范围,看是否能到终点。

Click to expand the code。解题的关键在于什么情况下步数+1.局部最优:当前可移动距离尽可能多走,如果还没到终点,步数再加一。整体最优:一步尽可能多走,从而达到最少步数。
用最少数量的箭引爆气球

Click to expand the code.关键在于需要更新右边界,不能单纯对比,因为必须满足每个最小右边界能被碰到!
无重叠区间

Click to expand the code.按照左边界排序。时间复杂度:O(nlog n) ,有一个快排。空间复杂度:O(n),有一个快排,最差情况(倒序)时,需要n次递归调用。因此确实需要O(n)的栈空间
Click to expand the code。若按照右边界排序,本质上好像是一样的,只是左边界排序个人感觉更好理解~
划分字母区间

Click to expand the code。时间复杂度O(N),空间复杂度O(1)
合并区间
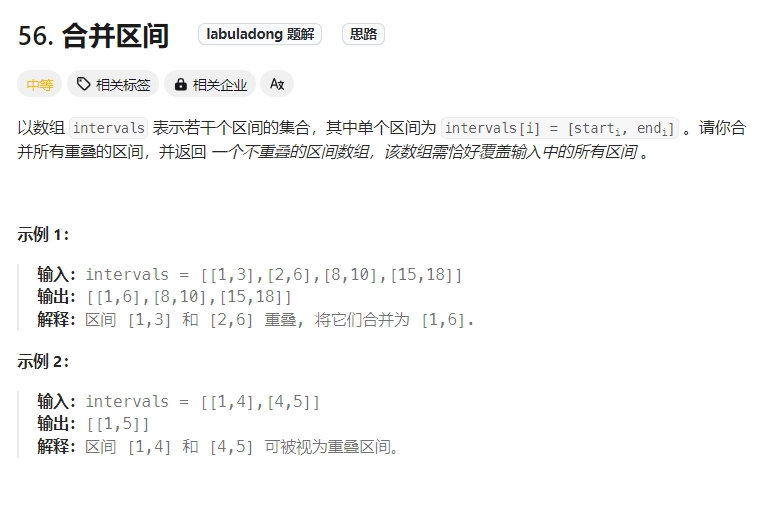
Click to expand the code。解题思路跟上面几题是很像的。时间复杂度: O(n+nlogn)。空间复杂度: O(logn),排序需要的空间开销
单调递增的数字

Click to expand the code。时间与空间复杂度都为O(N)
监控二叉树
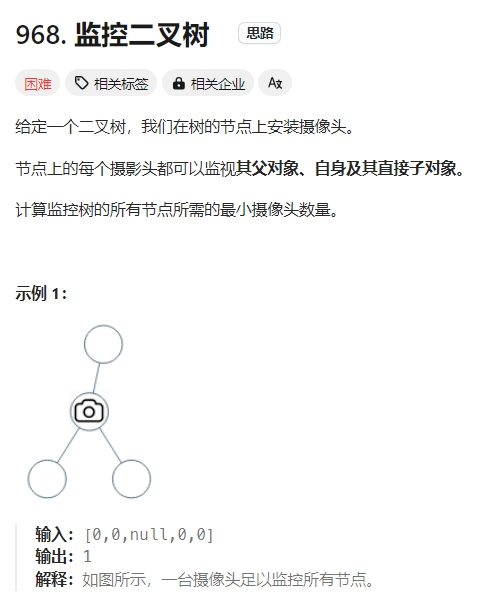
Click to expand the code。从下往上看,局部最优:让叶子节点的父节点安摄像头,所用摄像头最少,整体最优:全部摄像头数量所用最少!由于采用先从叶节点向上找,为此是后续历遍。