引言
之前做过不少动态规划方面的题目,但是都没有系统的整理,本博文系统整理下动态规划相关的知识。
动态规划算法(Dynamic Programming,简称 DP).它将一个问题分解为一系列更小的子问题(重叠子问题),并通过存储子问题的解来避免重复计算,从而大幅提升时间效率。
故此,动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心算法Link,贪心没有状态推导,而是从局部直接选最优的,
动态规划问题是从底到顶,而递归算法是从顶到底。
动态规划问题的一般形式就是求最值,而求最值的核心其实就是穷举,所谓的穷举就是定义好「状态转移方程」。
但是穷举所有可行解其实并不是一件容易的事,只有列出正确的「状态转移方程」,才能正确地穷举。同时对于状态与选择的定义也是很重要的。
为此,在本博文中,解题思路都是以三步走的方式来解决问题的。
1.定义dp表(注意下标含义),确定状态与选择。
2.确定初始状态。(边界值)。
3.确定状态转移方程,进行状态递推,自下向上(确定遍历顺序)。
PS:动态规划算法的一些手写笔记:



爬楼梯
1.自下而上,推到状态方程
首先通过经典的爬楼梯问题,导出其对应的动态规划解法
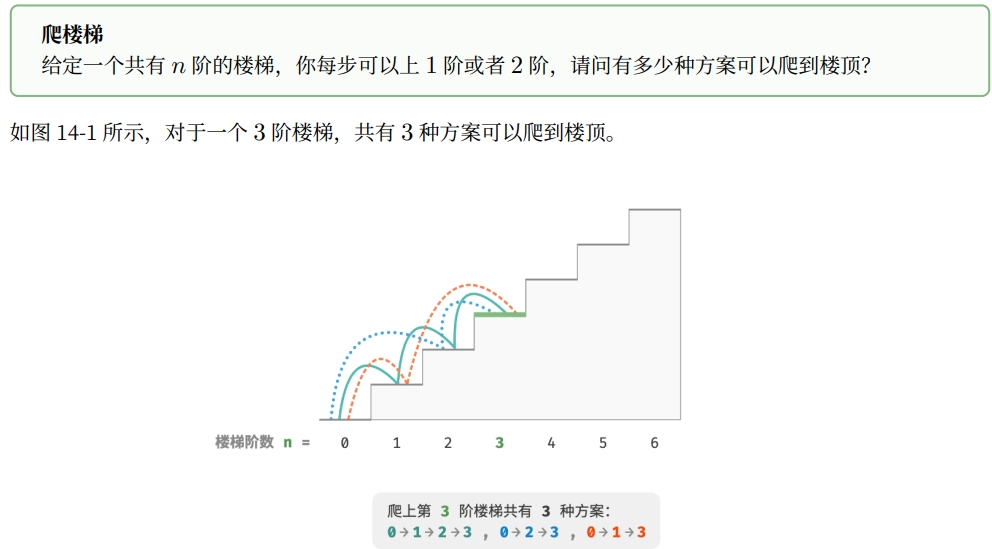
动态规划是一种“从底至顶”的方法:从最小子问题的解开始,迭代地构建更大子问题的解,直至得到原问题的解。
/* 爬楼梯:动态规划 */
int climbingStairsDP(int n) {
if (n == 1 || n == 2)
return n;
// step1: 初始化dp 表,用于存储子问题的解
vector<int> dp(n + 1);
// step1: 确定初始状态:预设最小子问题的解
dp[1] = 1;
dp[2] = 2;
// step3:确定状态转移方程,进行状态转移:从较小子问题逐步求解较大子问题
for (int i = 3; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];//状态转移方程
}
return dp[n];
}
根据上面的代码,可以简单总结出动态规划问题的解题思路:
- step1:初始化dp表。将数组𝑑𝑝称为𝑑𝑝表,𝑑𝑝[𝑖] 表示状态 𝑖 对应子问题的解。
- step2:确定初始状态。将最小子问题对应的状态(第 1 阶和第 2 阶楼梯)称为初始状态。
- step3:构建状态转移方程。将递推公式 𝑑𝑝[𝑖] = 𝑑𝑝[𝑖 − 1] + 𝑑𝑝[𝑖 − 2] 称为状态转移方程。
下面看看例题

Click to expand the code。时间复杂度O(N),空间复杂度为O(N)
class Solution {
public:
int climbStairs(int n) {
// n个阶梯对应多少种方法(一共n+1个元素),也就是状态dp
if(n<3)//要大于等于3才适用于动态规划的问题~
return n;
// 时间复杂度O(N),空间复杂度为O(N)
// step1:定义dp表
int dp[n+1];//n个状态,对应n+1数组
// step2:定义初始状态
dp[0]=0;
dp[1]=1;
dp[2]=2;//一次性两级,或两次1级,故此有两种方法
// step3:状态转移方程
for(int i=3;i<n+1;i++)//注意数组是到n+1
{
//第n级。有n-1或n-2决定
dp[i]=dp[i-1]+dp[i-2];//状态转移方程。
}
return dp[n];//最后返回第n阶梯的时候的解决方案
}
};
下面是等效的~
2.最优子结构
上图仅仅是展示了动态规划的基本构建,但是一般来说,动态规划都是用来解决最优化问题的,因此进一步的,题目形如下面:
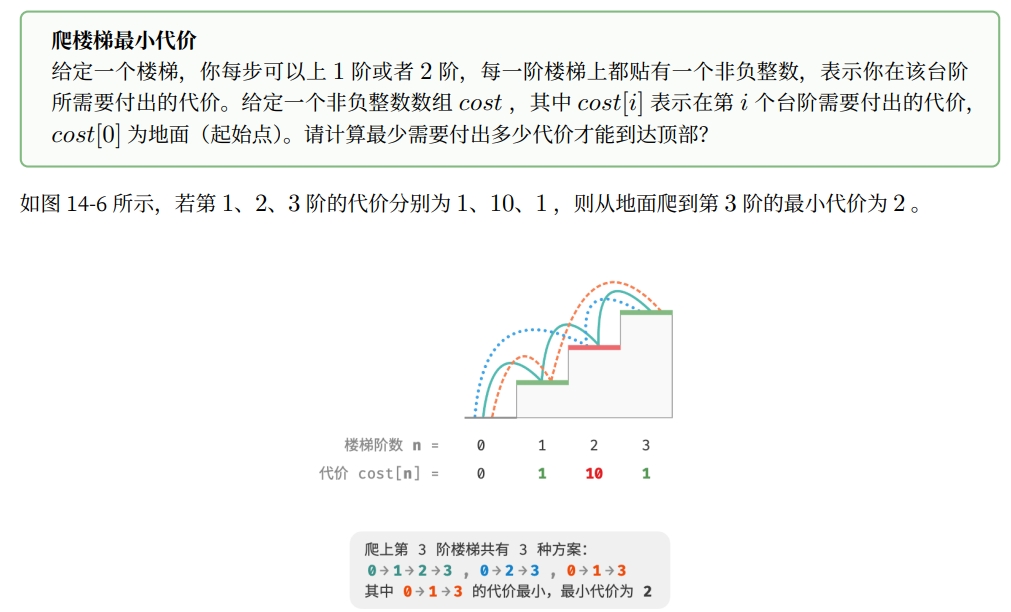
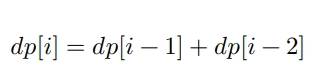
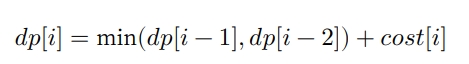
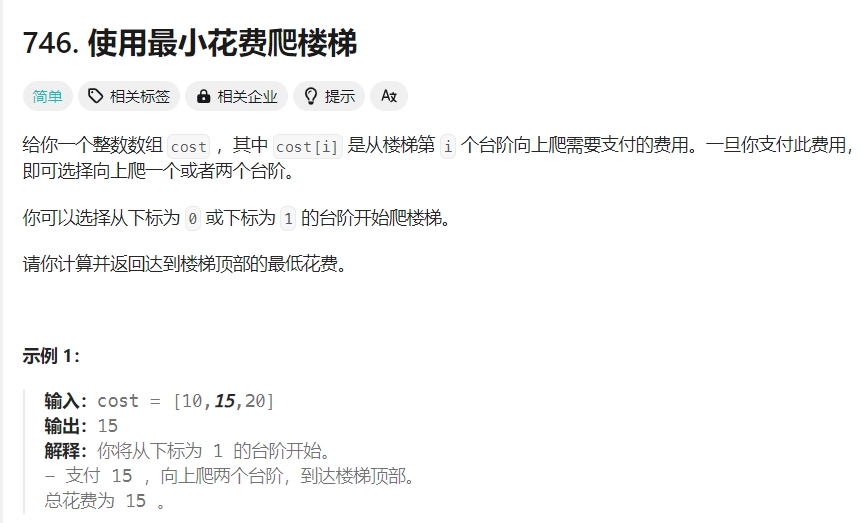
因此,这个带有最优子结构的动态规划问题应该如下代码所示:
/* 爬楼梯最小代价:动态规划 */
int minCostClimbingStairsDP(vector<int> &cost) {
int n = cost.size() - 1;
if (n == 1 || n == 2)
return cost[n];
// 初始化 dp 表,用于存储子问题的解
vector<int> dp(n + 1);
// 初始状态:预设最小子问题的解
dp[1] = cost[1];
dp[2] = cost[2];
// 状态转移:从较小子问题逐步求解较大子问题
for (int i = 3; i <= n; i++) {
dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i];
}
return dp[n];
}
下面看看例题
Click to expand the code
Click to expand the code。另外一种解法(可以理解为第一步花费,最后一步不花费,是旧版这个题目的描述)
3.带约束导致无后效性时,需要额外添加状态来保证
若进一步的,对上面题目添加限制条件,如下:
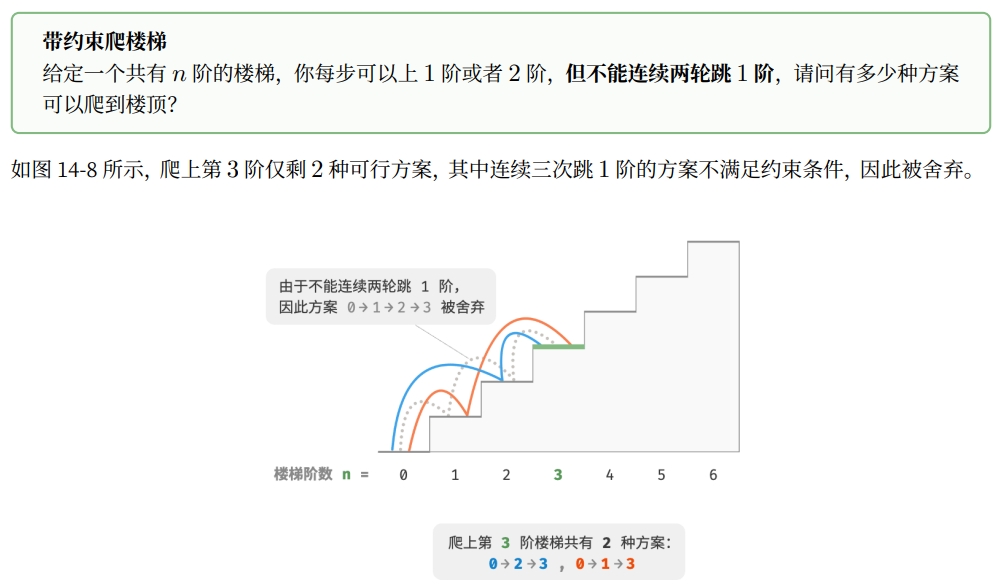
在此新问题中,下一步选择不能仅仅由当前状态(当前所在楼梯阶数)独立决定,还和前一个状态(上一轮所在楼梯阶数)有关。
因此不满足无后效性,那么上面的状态转移方程就不适用了。
又或者说:影响当前结果的,不再是一个状态,而是两个状态(当前的阶梯数,以及上次是走1级还是2级)。
为此,扩展状态定义:状态 [𝑖, 𝑗] 表示处在第 𝑖 阶并且上一轮跳了 𝑗 阶,其中 𝑗 ∈ {1, 2} 。此状态定义有效地区分了上一轮跳了 1 阶还是 2 阶,我们可以据此判断当前状态是从何而来的。
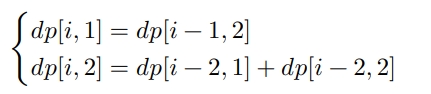
- 当上一轮跳了 1 阶时,上上一轮只能选择跳 2 阶,即 𝑑𝑝[𝑖, 1] 只能从 𝑑𝑝[𝑖 − 1, 2] 转移过来。
- 当上一轮跳了 2 阶时,上上一轮可选择跳 1 阶或跳 2 阶,即 𝑑𝑝[𝑖, 2] 可以从 𝑑𝑝[𝑖−2, 1] 或 𝑑𝑝[𝑖−2, 2] 转移过来。
代码如下:
/* 带约束爬楼梯:动态规划 */
int climbingStairsConstraintDP(int n) {
if (n == 1 || n == 2) {
return 1;
}
// 初始化 dp 表,用于存储子问题的解
vector<vector<int>> dp(n + 1, vector<int>(3, 0));
// 初始状态:预设最小子问题的解
dp[1][1] = 1;
dp[1][2] = 0;
dp[2][1] = 0;
dp[2][2] = 1;
// 状态转移:从较小子问题逐步求解较大子问题
for (int i = 3; i <= n; i++) {
dp[i][1] = dp[i - 1][2];
dp[i][2] = dp[i - 2][1] + dp[i - 2][2];
}
return dp[n][1] + dp[n][2];//两者之和代表爬到第 𝑛 阶的方案总数
}
递归vs动态规划:斐波那契数列

解法1:动态规划Click to expand the code。时间复杂度O(N),空间复杂度为O(N)
class Solution {
public:
int fib(int n) {
//首先只有大于2才适用
if(n<2)
return n;
//step1:定义dp表及下标的含义。
//状态就是当前在第几个数,选择就是前面两个数的和
int dp[n+1]; //对应于状态n
// step2:状态的初始化
dp[0]=0;
dp[1]=1;
// step3:自下而上遍历,推到状态方程
for(int i=2;i<n+1;i++)
{
dp[i]=dp[i-1]+dp[i-2];//后面的每一项数字都是前面两项数字的和
}
return dp[n];
}
};
用递归的思路解题也很简单。但是这个递归调用次数类似于计算一棵二叉树的节点数,树的高度为𝑛所以总的子树数目是O(2N),对应的时间复杂度为O(2N)。空间复杂度主要由递归调用的栈空间决定。每次递归调用都会占用一定的栈空间,递归的最大深度为𝑛,因此空间复杂度为:𝑂(N)
class Solution {
public:
int fib(int n) {
//首先只有大于2才适用
if(n<2)
return n;
return fib(n-1)+fib(n-2);
}
};
上面递归方法如果改为带有【备忘录】的写法,时间复杂度就会降低到O(N),所谓的备忘录写法其实就是对于每个结果都先记录着,如果这个结果被计算过了,就不重新计算,直接获值。也就是说动态规划其实就是相当于带有【备忘录】的递归。只是一个是自下而上,一个是自上而下。
带有【备忘录】的递归
对于上面解法1的动态规划解法。进一步的把空间复杂度降为 O(1)。当前状态 n 只和之前的 n-1, n-2 两个状态有关,其实并不需要那么长的一个 DP table 来存储所有的状态
class Solution {
public:
int fib(int n) {
//首先只有大于2才适用
if(n<2)
return n;
//step1:定义dp表
// int dp[n+1]; //对应于状态n
// step2:状态的初始化
// dp[0]=0;
// dp[1]=1;
int dp_i_2=0;
int dp_i_1=1;
// step3:自下而上,推到状态方程
for(int i=2;i<n+1;i++)
{
// dp[i]=dp[i-1]+dp[i-2];//后面的每一项数字都是前面两项数字的和
int dp_i=dp_i_1+dp_i_2;
// 滚动更新
dp_i_2=dp_i_1;
dp_i_1=dp_i;
}
// return dp[n];
return dp_i_1;
}
};
最大子数组和

Click to expand the code。动态规划解法。时间复杂度为O(N),空间复杂度为O(N)
Click to expand the code。贪心算法的解法,当前“连续和”为负数的时候立刻放弃,从下一个元素重新计算“连续和”,因为负数加上下一个元素 “连续和”只会越来越小。时间复杂度为O(N),空间复杂度为O(1)
最长递增子序列
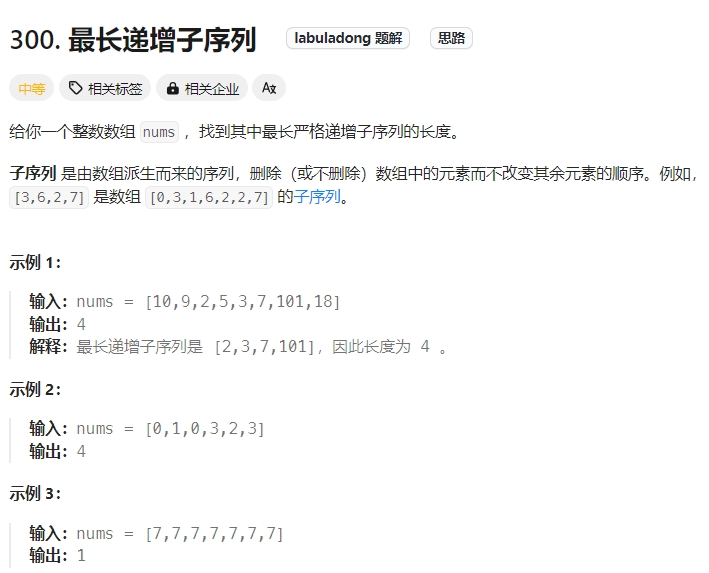
Click to expand the code。用了两个for循环,时间复杂度为O(N2),空间复杂度为O(N)也就是存储的dp表
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
// step1:定义dp表。状态变量应该就是n=nums.size()了吧,也是唯一的变量
int n=nums.size();
int dp[n];
// step2:确定初始状态
for(int i=0; i<n;i++)
{
dp[i]=1;//自身,长度就是1了
}
// step3:状态转移方程
// 对于状态dp[i]。以及在i前的状态j。
// 若nums【i】>nums【j】.那么dp【i】为dp【i】(其他值)与dp【j】+1之间的最值
int max_len=1;
for(int i=0;i<n;i++)
{
for(int j=0;j<i;j++)
{
if(nums[i]>nums[j]) //注意nums只能访问到n-1
dp[i]=max(dp[i], dp[j]+1);//循环的其他j也参与了对比的。只是只记录最大值
}
max_len=max(max_len,dp[i]);//dp[i]为最大的
}
return max_len;//不能直接返回dp[n-1],因为这是n-1位置时最大的,不是全部最大的~
}
};
Click to expand the code(用vector方便初始化,且涉及到循环对比的,需要先初始化,不然就会取空的时候的地址!)
最长连续递增序列

Click to expand the code。注意要连续的
Redraiment的走法
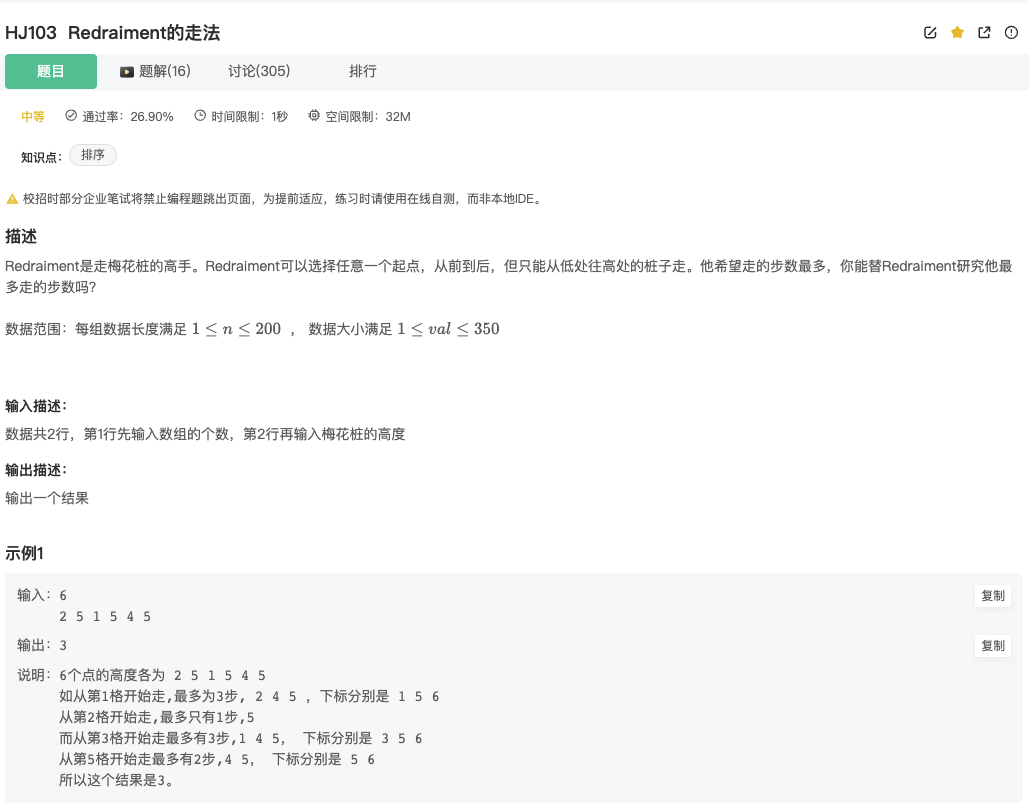
Click to expand the code。有点类似最长递增子序列
合唱队:最长递增子序列与最长递减子序列的结合
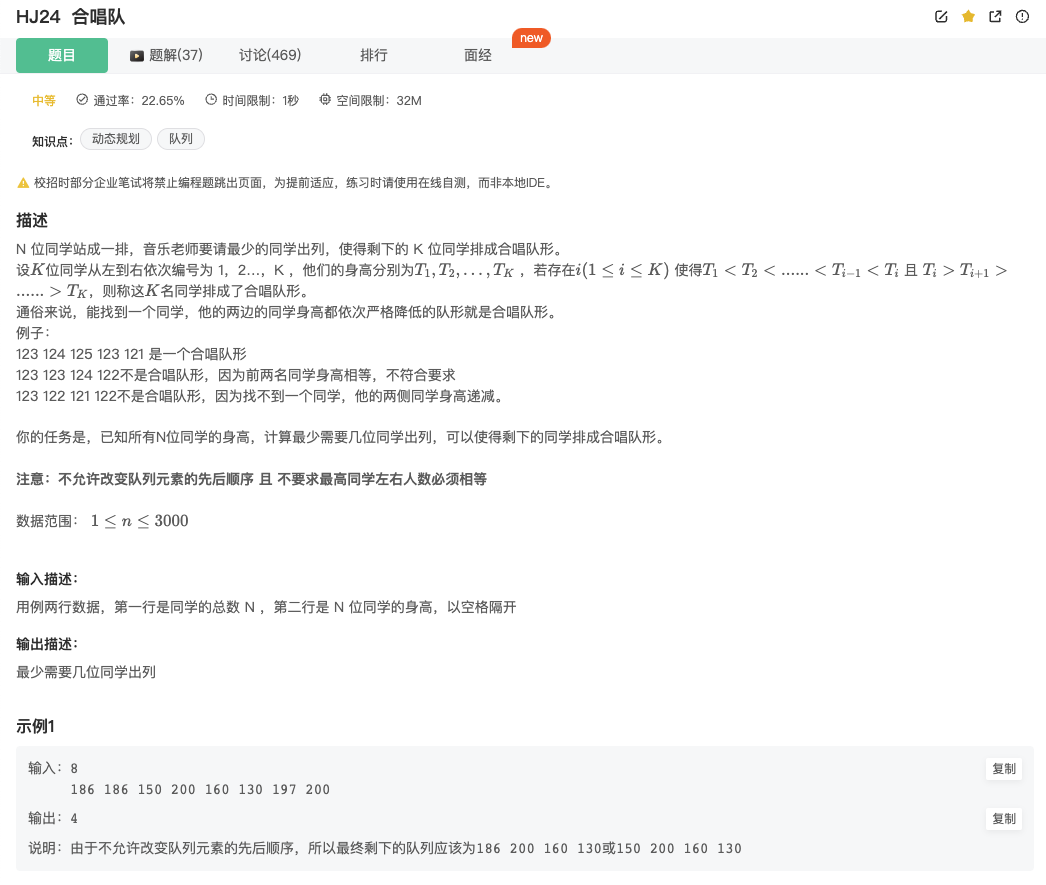
Click to expand the code
二维最长递增子序列:俄罗斯套娃信封问题

此题相当于最长递增子序列的二维版本,但是需要对数组先进行排列。但是leetcode上下面代码运行会超时,只能通过85/87.时间复杂度为O(N2),空间复杂度为O(N)
Click to expand the code。二分法解题将复杂度降低为O(NlogN)这个方法还不是很熟悉~
整数拆分

Click to expand the code.某种程度上跟最长递增子序列的结构是一样的。解题的关键在于设计的状态是拆分数字i,而不是拆分为i个。只有这样才满足递推关系。其次就是对于每个数有拆与不拆两种选择
同时维护两个一维的dp表:摆动序列

Click to expand the code
此题也可以用贪心算法来解决Link
二维动态规划问题,走格子
不同路径

Click to expand the code。机器人从(0 , 0) 位置出发,到(m - 1, n - 1)终点。这点最重要!
走方格的方案数
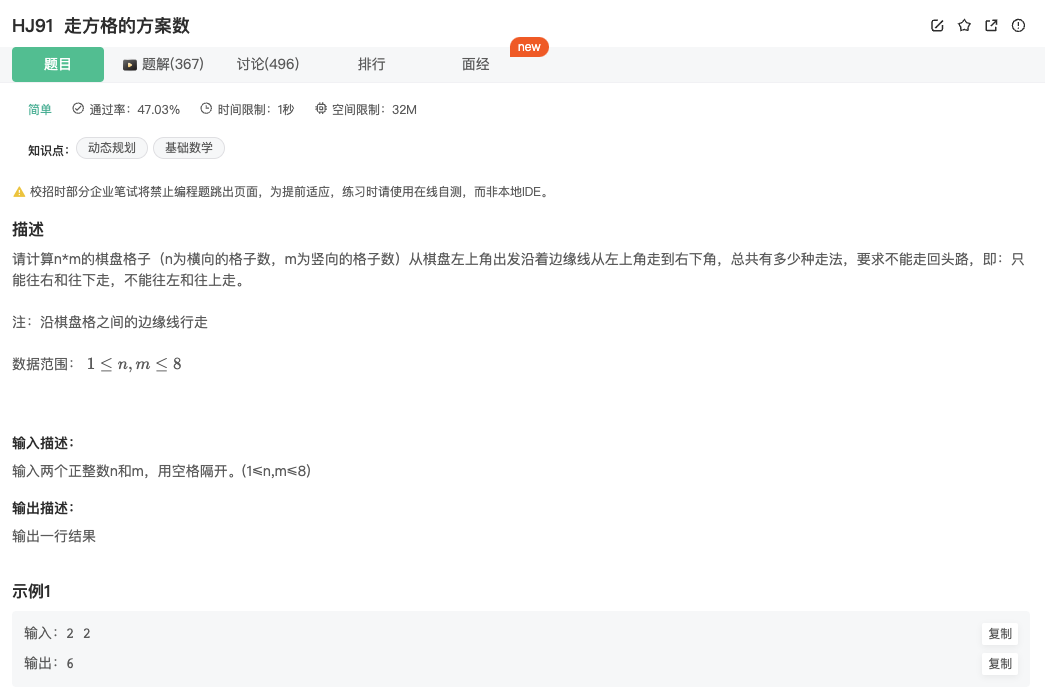
Click to expand the code。如若按照上一题的思路,此题应该是有问题的,n,m的格子。终端是(n-1,m-1)
不同路径 II

Click to expand the code。有障碍物处不能走,因此次数为0
下降路径最小和

Click to expand the code。时间与空间复杂度都是O(N2)
最小路径和

Click to expand the code。dp表的初始化容易出错,对于第i行第j列的dp标索引应该从0开始,从1开始其实也可以只是对应处理更加复杂而已~
逆向思维动态规划:地下城游戏

第一次解题的时候,想着把最小路径和改为最大路径和然后简单的对结果值进行修正希望达到最优。但实际上运行发现会选择运行28的结果。所以应该做到是损失最小,也就是负数之和最大,但是这个思路也不对,实际上就是同时考虑补充和扣减,与其如此,还不如换个思路,从右下角到左上角
两个字符串的动态规划问题
判断子序列
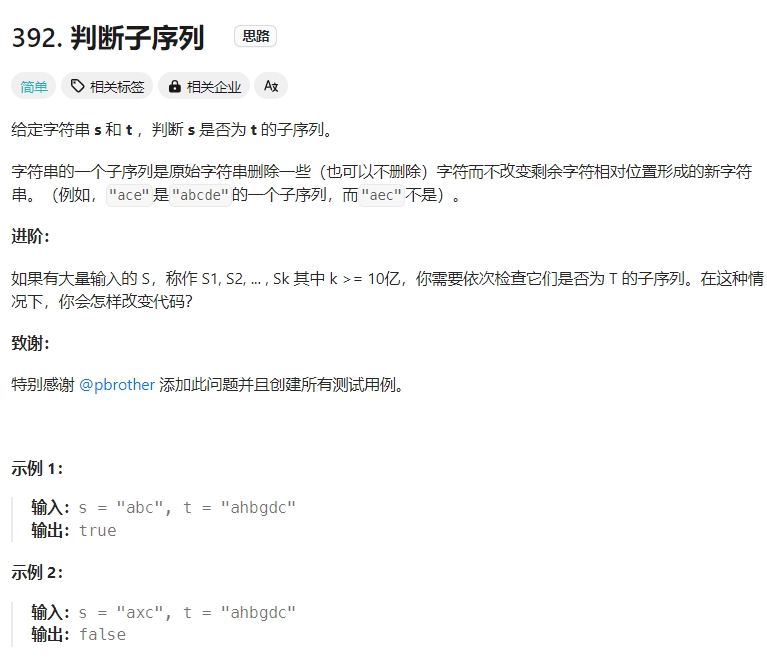
Click to expand the code。编辑距离入门级题目。本质上就是只有删除这一个操作
不同的子序列

Click to expand the code。也是编辑距离类型的题目,但只有删除的操作
两个字符串的删除操作

Click to expand the code。只是上面一题的进阶版,改为两个字符都可以删减了~
编辑距离

解决两个字符串的动态规划问题,一般都是用两个指针 i, j 分别指向两个字符串的最后,然后一步步往前移动,缩小问题的规模。(注意思路是往前移动,但实际上计算过程是往后移动,因为动态规划是自底向上的~)
Click to expand the code。(此题中,注释相对比较规范化了动态规划问题的解题~)时间复杂度O(M*N),空间复杂度为O(M*N)
字符串通配符
Click to expand the code,跟字符串编辑距离很像,只是有了其他字符因此对初始化会有影响!
回文子串

Click to expand the code。双指针法比较直接,见下题最长回文子串,此处仅用动态规划来解题
Click to expand the code。以i为起点,j为终点(这个思路更好理解~)
最长回文子串
动态规划解法,时间复杂度与空间复杂度都是O(N^2)。对于此类形的题目,定义的dp表应该为dp[j][i]:j代表了起点,i代表了终点。对比是否回文子串的过程就是dp[j][i]=(i++j && dp[j+1][i-1]).同时注意奇数与偶数的情况(aba与aa都是回文子串)
Click to expand the code。也可以采用双指针解法。时间复杂度是O(N^2)更上面一样的。但空间复杂度更小,为O(1)
最长回文子序列

Click to expand the code.以i为起点,j为终点
公共子串计算
最简单直接了当的方法应该是从最长的序列开始递减计算
这里也给出动态规划的解法
最长重复子数组

Click to expand the code。跟最长公共子串是一样的解题思路~
最长公共子序列

Click to expand the code。注意要的是子序列,不是子串。不要求连续的了,只是需要有相对顺序
不相交的线

Click to expand the code。直线不能相交,这就是说明在字符串A中 找到一个与字符串B相同的子序列,且这个子序列不能改变相对顺序,只要相对顺序不改变,链接相同数字的直线就不会相交。(本质上跟上一题“最长公共子序列”是一模一样的)
背包问题
背包问题有以下分类:
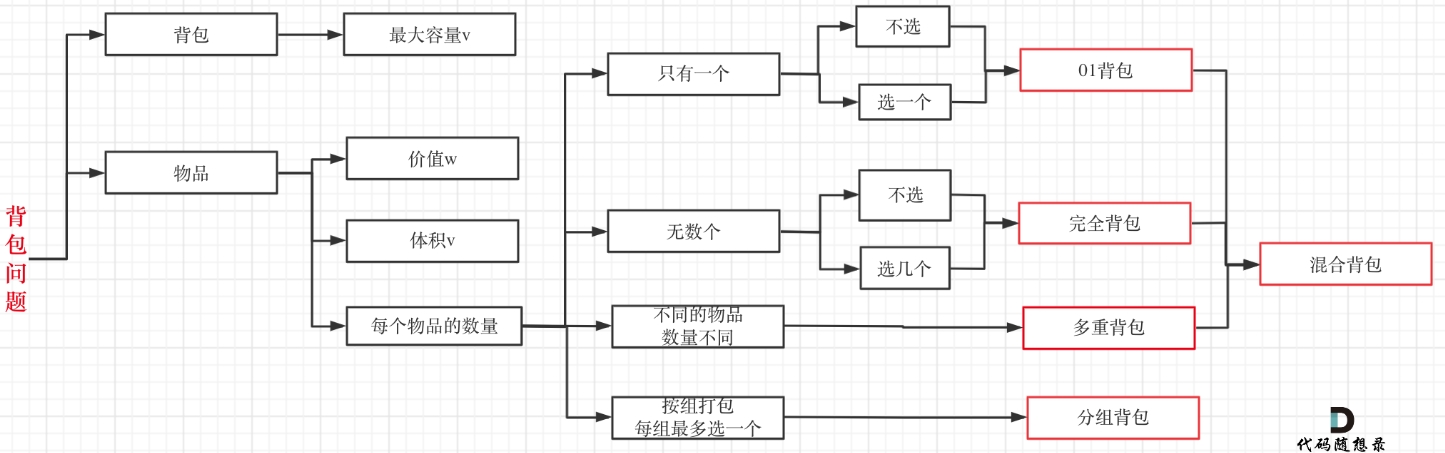
0-1背包问题
题目:给你一个可装载重量为 W 的背包和 N 个物品,每个物品有重量和价值两个属性。其中第 i 个物品的重量为 wt[i],价值为 val[i]。现在让你用这个背包装物品,每个物品只能用一次,在不超过被包容量的前提下,最多能装的价值是多少?
首先要明确两点,「状态」和「选择」。
第二步需要确定初始的状态。那么就是dp[0][..] = dp[..][0] = 0,因为没有物品或者背包没有空间的时候,能装的最大价值就是 0。
第三步就是确定状态转移方程(其实也就是上面「首先」的时候完成的了)
背包问题变体之子集分割/子集背包问题/分割等和子集

用递归的思路去解题不是不行,数组多了就会超出时间限制,当然也可以用回溯算法中的“划分为k个相等的子集”(还没尝试)
采用动态规划.一个商品如果可以重复多次放入是完全背包,而只能放入一次是01背包.而本题是每个元素只能用一次,因此属于01背包问题
最后一块石头的重量II

Click to expand the code。跟分割等和子集非常像,只是前者是判断是否均分,此处是判断最多放了一半多少(那么总的减去一半*2就是剩余的)
此外,注意sum需要初始化为0,对于涉及到遍历,特别是循环调用而不是单纯赋值的,一般都需要初始化,此外,可通过debug模式一步一步输出value查看bug
目标和

Click to expand the code.看到这道题的第一思路就是采用回溯算法,跟组合和有点类似。注意终止条件应该是index==nums.size()而不是index==nums.size()-1
Click to expand the code.当然,用动态规划去解题也是可以的。但是对于j为什么要从0开始理解得不是很透彻,且比回溯算法的思路复杂多了~
(PS:由于目标值会存在0,因此应该从0开始)
三维动态规划之一和零

Click to expand the code。关键在于分析问题进行数学建模
完全背包问题
所谓的完全背包问题是指:有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。
完全背包和01背包问题唯一不同的地方就是,每种物品有无限件。
01背包和完全背包唯一不同就是体现在遍历顺序上:
零钱兑换

如果用基本的动态规划问题的思路去解题。此处引出动态规划问题中状态以及选择量的确定过程:
1、确定「状态」,也就是原问题和子问题中会变化的变量。
由于硬币数量无限,硬币的面额也是题目给定的,只有目标金额会不断地向 base case (凑够了目标金额,为0)靠近,所以唯一的「状态」就是目标金额 amount。
2、确定「选择」,也就是导致「状态」产生变化的行为。
目标金额为什么变化呢,因为你在选择硬币,你每选择一枚硬币,就相当于减少了目标金额。所以说所有硬币的面值,就是的「选择」。
3、明确 dp 数组的定义。
即题目要求的凑出目标金额所需的「最少硬币数量」,所以是最少的金币数量。
Click to expand the code.此题的难点就是用什么作为状态,如何确定dp表。
下面可能更好理解
但实际上也是一个完全背包问题。 两道题可以相互转换,“物品”对应“硬币”、“物品重量”对应“硬币面值”、“背包容量”对应“目标金额”。 优化目标相反,完全背包问题是要最大化物品价值,零钱兑换问题是要最小化硬币数量。 完全背包问题是求“不超过”背包容量下的解,零钱兑换是求“恰好”凑到目标金额的解。
下面看看完全背包问题的解法
零钱兑换 II

Click to expand the code,题目跟上面很类似的,但此处不是求最优子问题,求解是总共有多少数目可以填满,可以转换为背包问题
此处有一个细节点,是先遍历物体在遍历背包的容量(跟下面的组合总和 Ⅳ相反)
对于大部分的完全背包的两个for循环的先后顺序都是可以的。因为纯完全背包求得装满背包的最大价值是多少,和凑成总和的元素有没有顺序没关系,即:有顺序也行,没有顺序也行!
而本题要求凑成总和的组合数,元素之间明确要求没有顺序。
所以纯完全背包是能凑成总和就行,不用管怎么凑的。
假设:coins[0] = 1,coins[1] = 5。
那么就是先把1加入计算,然后再把5加入计算,得到的方法数量只有{1, 5}这种情况。而不会出现{5, 1}的情况。
但是如果把遍历背包容量放外面,背包容量的每一个值,都是经过 1 和 5 的计算,包含了{1, 5} 和 {5, 1}两种情况。此时算出来的其实就是排列数了!
当然也可以不用背包问题的思路去解题!但是思路相对有点绕~
组合总和 Ⅳ

Click to expand the code.第一个思路也是用回溯算法去解此题(相当于无重可复选的情况),但由于是排列情况,计算时间非常大,会导致超时
Click to expand the code.采用动态规划解题,注意也不能用《零钱兑换 II》中的解法1(背包问题)的思路去解题,因为顺序不一样,算不同的组合数!
如果把遍历nums(物品)放在外循环,遍历target的作为内循环的话,举一个例子:计算dp[4]的时候,结果集只有 {1,3} 这样的集合,不会有{3,1}这样的集合,因为nums遍历放在外层,3只能出现在1后面!
所以本题遍历顺序最终遍历顺序:target(背包)放在外循环,将nums(物品)放在内循环,内循环从前到后遍历。
Click to expand the code.用一维数组也可以解决,但是如果是int的话可能越界,因此用long形
完全平方数

Click to expand the code
单词拆分

Click to expand the code.跟顺序有关,故此必然是先遍历背包,再遍历物体
同时注意是 dp[wordDict.size()][j-wordDict[i-1].size()]而不是 dp[i][j-wordDict[i-1].size()],因为是从所有的单词中找,而不是当前的单词中找
多重背包
有N种物品和一个容量为V 的背包。第i种物品最多有Mi件可用,每件耗费的空间是Ci ,价值是Wi 。求解将哪些物品装入背包可使这些物品的耗费的空间 总和不超过背包容量,且价值总和最大。
这就是典型的多重背包问题,但是本质上还是01背包问题,只是在01背包问题的基础上,每个物品的数量不再是1个,而是有多个。每件物品最多有Mi件可用,把Mi件摊开,其实就是一个01背包问题了。
分组背包问题:购物单

这道题其实就是在01背包问题的基础上,添加了各种约束。使得整体比较复杂。解题的关键点是:
1、每次只处理主件。如果是附件的话,状态等于上一次。
2、所谓的状态分为:不买、买主件、买主件+1个附件、买主件+2个附件。只有四个状态。而不买跟当前是附件的状态一样,都是继承上一个状态
3、在讨论买主件、主件+1附件、主件+2附件的时候,是依次递推满足的情况下再记录状态,不然会超时。
打家劫舍系列问题
打家劫舍

Click to expand the code
Click to expand the code.另一种解法:两个一维数组的动态规划
打家劫舍II

Click to expand the code
打家劫舍 III
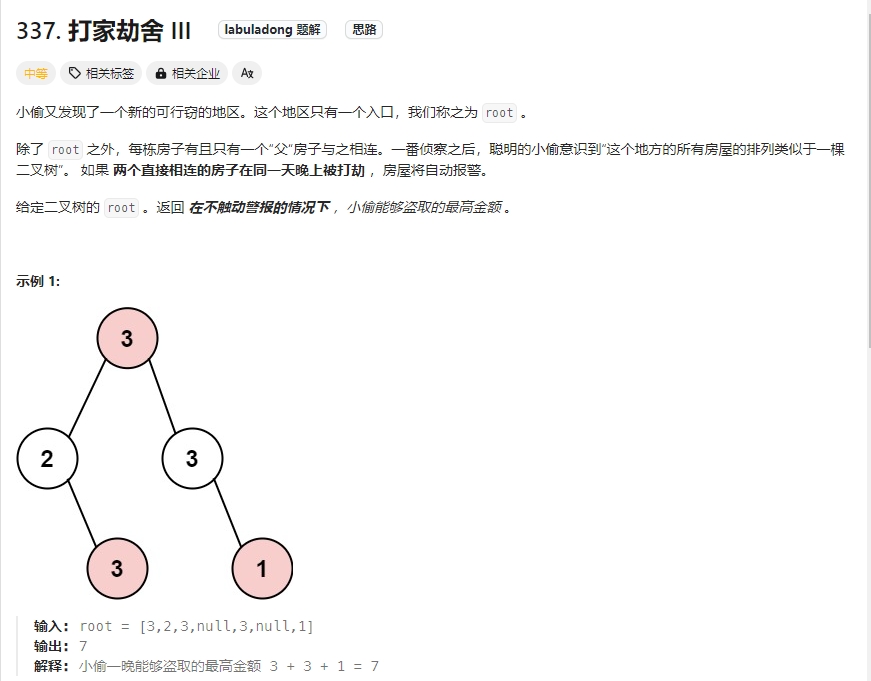
Click to expand the code。本题其实是在上面两题的基础上把数据结构改成了树的形式
对于树的话,首先就要想到遍历方式,前中后序(深度优先搜索)还是层序遍历(广度优先搜索)。详细请见博客Link
注意vector{0,0} 或vector a(2,0) 都是两个0的vector,
(三维动态规划/两个二维动态规划)买卖股票的最佳时机系列问题
这部分主要参考:一个方法团灭 LeetCode 股票买卖问题,不过原文确实写得比较差,此处给出本人总结的思路.
k次交易

Click to expand the code
一次交易

Click to expand the code。此题相当于,只进行一次交易,相当于题目188中的 k = 1
Click to expand the code。化简代码的写法
无限次交易

Click to expand the code。此题相当于题目188中的无限次交易。注意此处跟121题的区别其实只是当前持有时dp[i][1],如果当前时买了,是否应该考虑之前的状态!只有一次交易则不用考虑,因为之前肯定不持有股票(必然没钱),但是如果时无限次交易则必须要考虑之前不持有股票的情况了(有可能已经有利润)。
无限次交易+冷冻期

Click to expand the code。关键只是冷冻期就必须考虑当前持有可以是上次不持有然后当前买入。但是上次不持有就只能是上次的上次本来就不持有,而不能是上次卖出导致不持有,因为有冷冻期。因此需要针对i-2的情况额外初始化dp表
无限次交易+手续费

Click to expand the code。只是在上一刻持有并当前需要卖出的时候,考虑手续费即可
只进行2次交易,k=2

Click to expand the code.只是188题目中k=2的特例而已。当然此题也有简化版本,其实也就是把k的情况给列出来,不用维护数组而已,但是本人觉得还是应该按K次来计算,不然重新维护,更乱!