Catalog

回溯算法和二叉树的递归（DFS）算法非常类似，本质上就是一种暴力穷举算法。它的核心思想是从一个初始状态出发，暴力搜索所有可能的解决方案，当找到正确解的时候就将其记录，直到找到所有。
注意：回溯算法跟动态规划一样，都是一种穷举的方式，但是不一样的是，动态规划一般是求最值（最优解），而回溯算法一般是求所有的可行解而非最值。
回溯算法的核心就是 for 循环里面的递归，在递归调用之前「做选择」，在递归调用之后「撤销选择」。


result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return //这也是一种回退
    
    for 选择 in 选择列表:
        做选择（尝试做这个选择）：前序位置

        backtrack(路径, 选择列表)

        撤销选择（退回到之前状态）：后序位置

下面框架更清晰些：

N 皇后问题

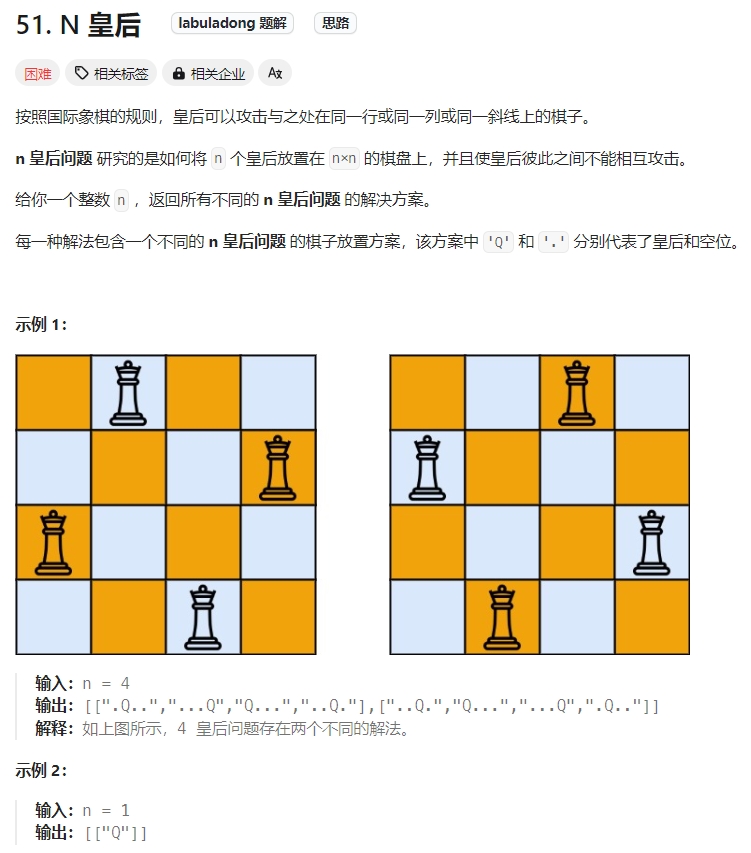
Click to expand the code。时间复杂度是O（N！）回溯算法中对应着For循环。空间复杂度：O(N)是递归栈，但是还有O（N²）是存放的结果占用的空间


  // 本题本质上就是，决策树的每一层表示棋盘上的每一行；每个节点可以做出的选择是，在该行的任意一列放置一个皇后

  class Solution {
  public:
      // 输入棋盘边长 n，返回所有合法的放置
      vector<vector<string>> solveNQueens(int n) {
  
          // 每个字符串代表一行，字符串列表代表一个棋盘
          // '.' 表示空，'Q' 表示皇后，初始化空棋盘
          vector<string> board(n, string(n, '.'));//将其初始化为空棋盘
          // 注意,对于board为n个string,每个string为n个字符
  
          vector<vector<string>> result;//结果(存放的所有结果)
          backtrack(board,result, 0);//一开始row为0
          return result;
      }
  
      // 路径：board 中小于 row 的那些行都已经成功放置了皇后
      // 选择列表：第 row 行的所有列都是放置皇后的选择
      // 结束条件：row 超过 board 的最后一行
      void backtrack(vector<string>& board, vector<vector<string>>& result, int row) 
      {
          //结束的条件
          if(row==board.size())
          {
              result.push_back(board);//将当前的结果存放
          }
  
          //对于当前row的每一列
          for (int col = 0; col < board[0].size(); col++)
          {
              //先判断是否合法(也就是说是否可以在board[row][col]上放置皇后)
              if (!isValid(board, row, col))
              {
                  continue;//若无效,那么就是当前位置不应该方
              }
              board[row][col]='Q';// 做选择
              backtrack(board,result, row+1);//回溯算法(一行一行的放，故此下面只需要检查列不用检查行)
              board[row][col]='.';// 撤销选择
  
          }
  
      }
  
      // 判断是否可以在 board[row][col] 放置皇后
      //因为皇后是一行一行从上往下放的，所以左下方，右下方和正下方不用检查（还没放皇后）；
      //因为一行只会放一个皇后，所以每行不用检查。也就是最后只用检查上面，左上，右上三个方向。
      bool isValid(vector<string>& board, int row, int col) 
      {
  
          //先检查在这一行前,当前列是否有皇后放置了（固定了列，行变，就是一列）
          for(int i=0;i<row;i++)
          {
              if (board[i][col]=='Q')//存在皇后
                  return false;
          }
  
          // 检查右上方.右上方就是当前row-1,col+1
          for(int i=row-1, j=col+1; i>=0 && j<board.size(); i--, j++)
          {
              if (board[i][j]=='Q')//存在皇后
                  return false;
          }
  
          //检查左上方.右上方就是当前row-1,col-1
          for(int i=row-1, j=col-1; i>=0 && j>=0; i--, j--)
          {
              if (board[i][j]=='Q')//存在皇后
                  return false;
          }
  
          return true;//都不满足则是true
  
      }
  };

解法跟上面是一样的，只是保存结果不一样而已~当然直接返回result.size()也可以，但是在某些测试下可能会内存超出限制，为此还是应该把返回的结果为int


  class Solution {
  public:
      // 输入棋盘边长 n，返回所有合法的放置
      int totalNQueens(int n) {
  
          // 每个字符串代表一行，字符串列表代表一个棋盘
          // '.' 表示空，'Q' 表示皇后，初始化空棋盘
          vector<string> board(n, string(n, '.'));//将其初始化为空棋盘
          // 注意,对于board为n个string,每个string为n个字符
  
          int result=0;//结果
          backtrack(board,result, 0);//一开始row为0
          return result;
      }
  
      // 路径：board 中小于 row 的那些行都已经成功放置了皇后
      // 选择列表：第 row 行的所有列都是放置皇后的选择
      // 结束条件：row 超过 board 的最后一行
      void backtrack(vector<string>& board, int& result, int row) 
      {
          //结束的条件
          if(row==board.size())
          {
              result+=1;//结果+1
          }
  
          //对于当前row的每一列
          for (int col = 0; col < board.size(); col++)
          {
              //先判断是否合法(也就是说是否可以在board[row][col]上放置皇后)
              if (!isValid(board, row, col))
              {
                  continue;//若无效,那么就是当前位置不应该方
              }
              board[row][col]='Q';// 做选择
              backtrack(board,result, row+1);//回溯算法
              board[row][col]='.';// 撤销选择
  
          }
  
      }
  
      // 判断是否可以在 board[row][col] 放置皇后
      bool isValid(vector<string>& board, int row, int col) 
      {
  
          //先检查在这一行前,当前列是否有皇后放置了
          for(int i=0;i<row;i++)
          {
              if (board[i][col]=='Q')//存在皇后
                  return false;
          }
  
          // 检查右上方.右上方就是当前row-1,col+1
          for(int i=row-1, j=col+1; i>=0 && j<board.size(); i--, j++)
          {
              if (board[i][j]=='Q')//存在皇后
                  return false;
          }
  
          //检查左上方.右上方就是当前row-1,col-1
          for(int i=row-1, j=col-1; i>=0 && j>=0; i--, j--)
          {
              if (board[i][j]=='Q')//存在皇后
                  return false;
          }
  
          return true;//都不满足则是true
  
      }
  };

排列/组合/子集问题

1.子集（元素无重不可复选）

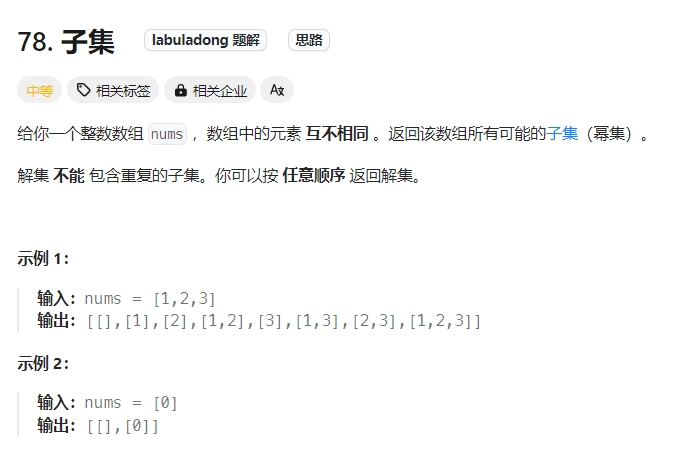
Click to expand the code.时间复杂度为O(N*2^N),空间复杂度为O（N）


  class Solution {
    public:
    
        // 定义回溯算法
        void backtrack(vector<int>& nums,  vector<int>& track, vector<vector<int>>& result, int index)
        {
            // 没有终止条件，每次应该就是把当前的track放入result中
            result.push_back(track);//放入结果
    
            for(int i=index;i<nums.size();i++)
            {
                // 前序的位置
                track.push_back(nums[i]);//放入
    
                // 回溯函数调用(这里index+1，表示不允许重复使用当前数字)
                backtrack(nums, track, result, i+1);//注意是i+1
    
                // 后序的位置
                track.pop_back();// 拿出来最后一个
            }
    
        }
    
        vector<vector<int>> subsets(vector<int>& nums) {
    
            // 注意：解集不能包含重复的子集。也就是不考虑顺序
            vector<vector<int>> result;//最终的结果
            vector<int> track;//每次结果
    
            backtrack(nums, track, result, 0);
            return result;
    
        }
    };

2.组合（元素无重不可复选）

与上一题的解题思路几乎一样


  class Solution {
    public:
    
        void backtrack(const int n, const int k, vector<vector<int>>& results, vector<int>& each_result, int index)
        {
            // 结束条件,当size为k时
            if(each_result.size()==k)
            {
                results.push_back(each_result);
            }
    
            // 遍历整个数组
            for(int i=index; i<=n;i++)//注意时闭区间,包含了n
            {
                // 前序位置
                each_result.push_back(i);
    
                // 回溯
                backtrack(n,k,results,each_result,i+1);//i的下一个
    
                //后序位置
                each_result.pop_back();//插入的用完后删掉
            }
        }
    
        vector<vector<int>> combine(int n, int k) {
    
            vector<vector<int>> results;
            vector<int> each_result;
            backtrack(n,k,results,each_result,1);//index为索引到的数字,从1开始
            return results;
        }
    };

组合总和III

Click to expand the code.注意要从1开始

分割回文串

Click to expand the code.本质上为子集问题。可重不可复选，只是额外需要判断是否回文子串（用于剪纸）

复原IP地址

Click to expand the code。跟上一题分割回文子串很像，只是额外多了要添加点的操作。
关键点在于额外构建函数每次判断字符是否合法的一位。合法就放入，然后继续回溯计算。下一次重新测[index，i]区间

3.排列（元素无重不可复选）

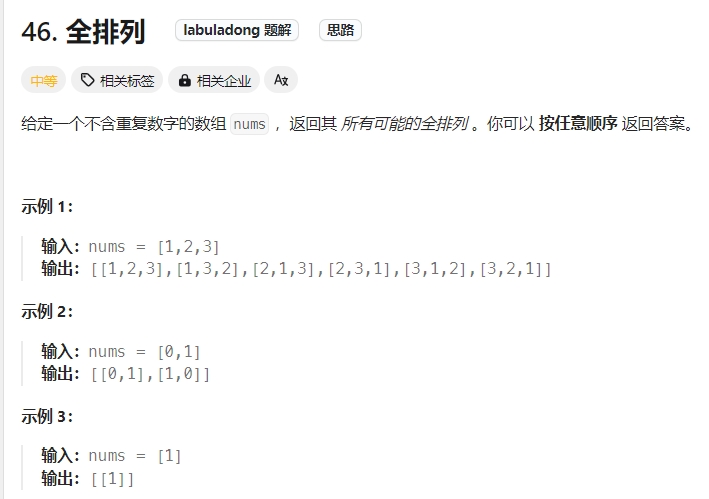
Click to expand the code。注意：此题的全排列问题不包含重复的数字，下一题则是包含重复数字。递归的时间复杂度为O（N！）加上递归中每个有for循环，故此应该是O（N*N！）。空间复杂度应该是O（N）

下面代码跟上面的区别只是上面通过索引index以及swap来保证交互的两个不会重复被用，此处用vector来记录是否被用过。本质上是一样的。以及递归空间复杂度也是O(N)所以并没有差别～

4.子集（元素可重不可复选）

通过新增的if判据，来实现元素虽然存在重复,但是最终结果不能管顺序。空间复杂度：O(n)。临时数组 t 的空间代价是 O(n)，递归时栈空间的代价为 O(n)。而时间复杂度。首先sort排序的时间复杂度为：O（N）回溯的时间复杂度为O(2^N),然后遍历每个字符，所以应该是O（N*2^N）至于前面排序sort的时间复杂度也是O（N），因此总的时间复杂度为O（N*2^N）

非递减子序列

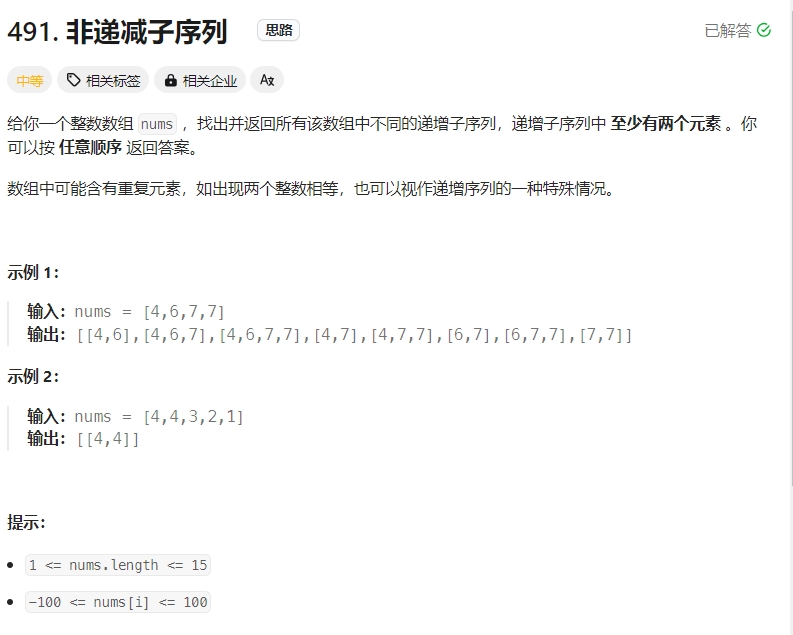
Click to expand the code。相当于取有序的子集（可重，不可复选）。但是跟上一题不一样的是不能对原数组进行排序的，因此其原本的去重的方式不适用。此处改为用find来看是否存在重复的结果。

Click to expand the code。另外一种解法，额外维护一个数组来标记是否重复，但注意是标记每一层（宽度）而非深度！！！

5.组合（元素可重不可复选）

Click to expand the code。组合跟子集问题时很类似的，故此解法基本一样~注意对于剩余target值的管理。等于0时返回，小于0时没必要继续计算，否则浪费计算时间~


  class Solution {
    public:
        void backtrack(vector<int>& candidates, int target, vector<vector<int>>& results,vector<int>& each_result, int index)
        {
            // 定义结束标致,当target为0时
            if(target==0)
            {
                results.push_back(each_result);
                return;
            }
            
            // 遍历整个数组
            for(int i=index;i<candidates.size(); i++)
            {
                // 满足条件进行剪枝,以此去重
                if(i>index && candidates[i]==candidates[i-1])//若当前值等于上一个值.同时除掉最开始的index以保证每次选重复值的第一个
                    continue;
    
                if(target-candidates[i]<0)//超出了(再继续计算已经没有意义了)
                    return; //或者break
                    
                //前序
                each_result.push_back(candidates[i]);
    
                backtrack(candidates, target-candidates[i],results,each_result,i+1);//注意不要漏掉每次减candidates[i]
    
                each_result.pop_back();//后序的位置上删掉
    
            }
        }
    
        vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
            // 存在重复的数字,但不能包含重复的组合(顺序变化不算)
            
            //先进行排序,这样有利于去重
            sort(candidates.begin(),candidates.end());
    
            vector<vector<int>> results;
            vector<int> each_result;
            backtrack(candidates, target,results,each_result,0);
            
            return results;
        }
    };

6.排列（元素可重不可复选）

Click to expand the code

也有一种情况是只需要输出一共的排列的数的，但用results数组的size会导致内存不够，为此用int来代替~

此题与上面1中的第46题不同的是包含了重复的字母，因此全排列可能包含重复的序列，故此需要去重。其余的解题思路跟上面是一样的


  class Solution {
    public:
    
        void calculate(vector<int>& nums, vector<vector<int>> &result, int first_index, const int len)
        {
            if(first_index==len-1)//到达了尾部
            {
                result.push_back(nums);
                return;
            }
    
            set<int> flag;//用于记录每次是否遍历过（在set中每个元素的值都唯一，因此可以判定当前这个数字有没有出现过！）
            for(int i=first_index;i<len;i++)
            {
                //满足某些情况下，跳过不处理
                if(
                    flag.find(nums[i])!=flag.end()//如果找到一样的
                ) 
                    continue;//就不处理了，跳过
                flag.insert(nums[i]);//每次插入新的
                swap(nums[i], nums[first_index]);//调换位置
                calculate(nums, result, first_index+1,len); // first_index可以理解为固定不变的位置，变的i为与其兑换进行全排列
                swap(nums[i], nums[first_index]);//换回来，继续下次
                
            }
        }
    
    
        vector<vector<int>> permuteUnique(vector<int>& nums) {
            vector<vector<int>> result;
            calculate(nums, result, 0, nums.size());
            return result;
        }
    };

7.组合（元素无重可复选）

原本采用递归的解法


  class Solution {
    public:
        void calculate(vector<vector<int>>& result_group,vector<int>& candidates, int target, vector<int>& temp, int index)
        {
            if(index==candidates.size())
                return;//最后一个了，跳出
            
            if(target==0)//找到了(放入结果并退出)
            {
                result_group.push_back(temp);
                return;
            }
    
            calculate(result_group,candidates,target,temp,index+1);//遍历每一个index
    
            // 同一个index下，遍历计算(会通过上面的更新)
            if(target-candidates[index]>=0)//大于0，可以继续计算
            {
                temp.push_back(candidates[index]);
                calculate(result_group,candidates,target-candidates[index],temp,index);
                temp.pop_back();//当前计算完就删掉
            }
        }
    
        vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
            //没有重复的数组,可以重复选择
    
            vector<vector<int>> result_group;
            vector<int> temp;
            // 不同于两数之和或三数之和，数目可以是随意的。
            // 采用递归的解法，对于选择了第i位，target=target-candidates[i],继续从candidates中找，直到target=0
            calculate(result_group,candidates,target,temp,0);
            return result_group;
            
        }
    };

上面方法的思路是可以实现的，但是不成体系，为此用回溯的框架看看


  class Solution {
    public:
        void backtrack(vector<vector<int>>& results,vector<int>& candidates, int target, vector<int>& each_result, int index)
        {
            
            // 定义结束条件
            if(target==0)//找到了(放入结果并退出)
            {
                results.push_back(each_result);
                return;
            }
    
            for(int i=index;i<candidates.size();i++)
            {
                if(target-candidates[i]<0)//接下来就无法算了,为此跳过这个节点
                    continue;
    
                each_result.push_back(candidates[i]);//前序
                // 由于可以多次选择,因此无需+1,每次都重新看
                backtrack(results,candidates,target-candidates[i],each_result,i);//无需i+1，那么当前的就可以被再次选择
                each_result.pop_back();//后序
            }
    
        }
    
        vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
            //没有重复的数组,可以重复选择
    
            vector<vector<int>> results;
            vector<int> each_result;
    
            backtrack(results,candidates,target,each_result,0);
            return results;
            
        }
    };

8.子集（元素无重可复选）

此类型目前还没找到例题

9.排列（元素无重可复选）

此类型目前还没找到例题

10.元素可重可复选

元素可重可复选。但既然元素可复选，那又何必存在重复元素呢？因此可以先对元素进行去重处理，然后就是退化为无重可复选的情况了。

有限制的回溯算法：火车进站

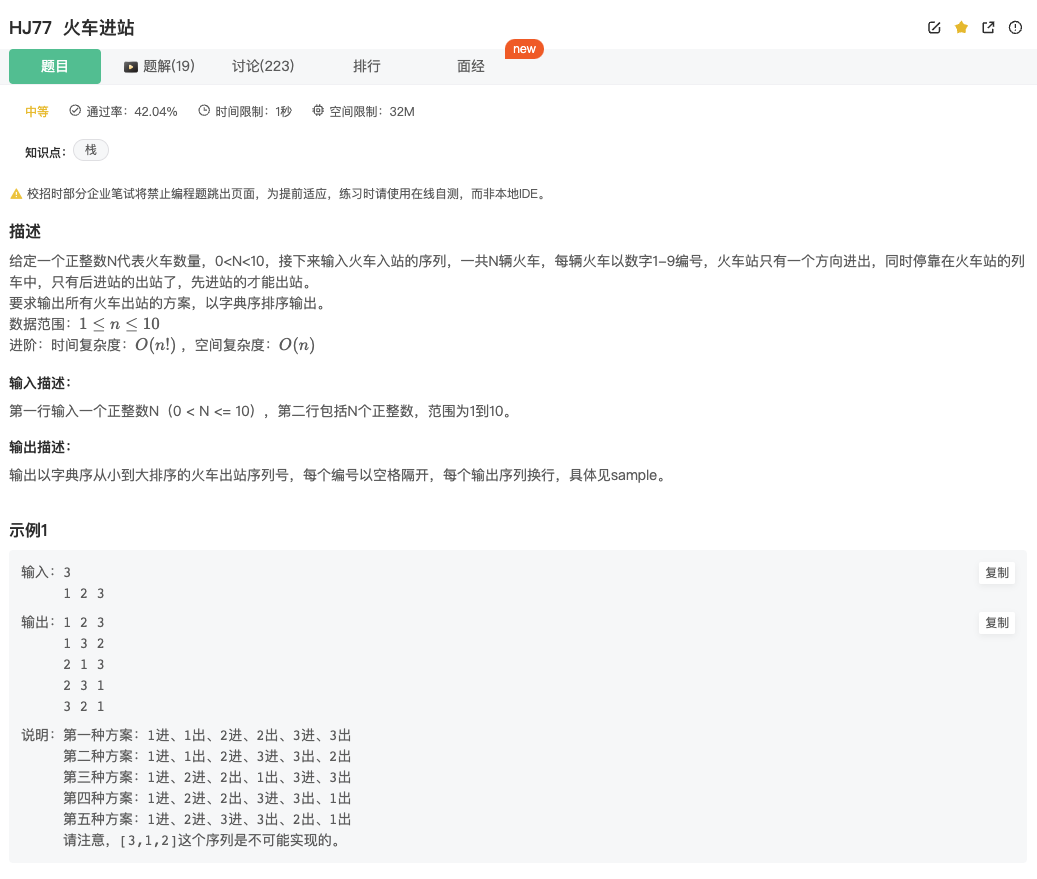
Click to expand the code。有两种选择的回溯算法，或者说有限制的回溯算法

有限制/有选择的回溯算法：括号生成

对于括号合法性的判断，主要是借助「栈」(详情请见博客^Link)，而对于括号的生成，一般都要利用回溯算法进行暴力穷举。

Click to expand the code。关键的解题点或者说约束点在于：对于一个「合法」的括号字符串组合 p，必然对于任何 0 <= i < len(p) 都有：子串 p[0..i] 中左括号的数量都大于或等于右括号的数量

解数独

Click to expand the code.这个回溯算法需要带return bool的，一找到结果马上停止进一步搜索。

划分为k个相等的子集

下面方法可以解决，但是计算量较大，没有办法通过所有的测试案例，即使添加了排序也不行

Click to expand the code。换个思路去实现，也不行，当然可以加上index，让i从index开始，这样可以通过更多样例，但最终还是超时

Click to expand the code。下面就是让i从index开始，这样可以通过更多样例，但最终还是超时

Click to expand the code。下面是最终的解决方法，参考别人的代码，找到了新的剪枝的策略！！！

这题其实跟下面牛客网的题目很像，只是牛客网的这道题要求3的倍数和5的倍数不能放一起。通过递归即可解决～

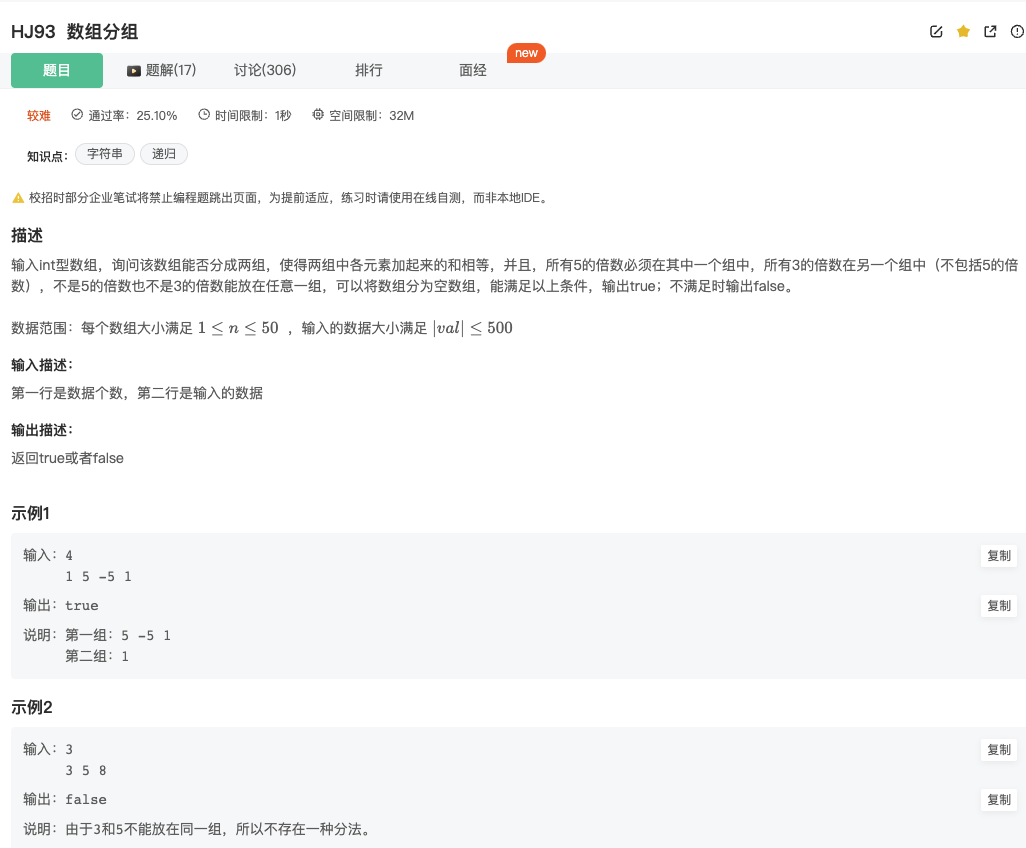
Click to expand the code.关键是分解问题的思路～

电话号码的数字组合

Click to expand the code。hash table与回溯算法的结合。

时间复杂度：O(3^m×4ⁿ )，其中 m 是输入中对应 3 个字母的数字个数（包括数字 2、3、4、5、6、8），n 是输入中对应 4 个字母的数字个数（包括数字 7、9），m+n 是输入数字的总个数。当输入包含 m 个对应 3 个字母的数字和 n 个对应 4 个字母的数字时，不同的字母组合一共有3^m×4ⁿ种，需要遍历每一种字母组合。
空间复杂度：O(m+n)，其中 m 是输入中对应 3 个字母的数字个数，n 是输入中对应 4 个字母的数字个数，m+n 是输入数字的总个数。除了返回值以外，空间复杂度主要取决于哈希表以及回溯过程中的递归调用层数，哈希表的大小与输入无关，可以看成常数，递归调用层数最大为 m+n。

目标和

Click to expand the code.看到这道题的第一思路就是采用回溯算法，跟组合和有点类似。注意终止条件应该是index==nums.size()而不是index==nums.size()-1

此题也可以用动态规划^Link去求解,但是思路比较绕，还是回溯算法比较直观。

重新安排行程

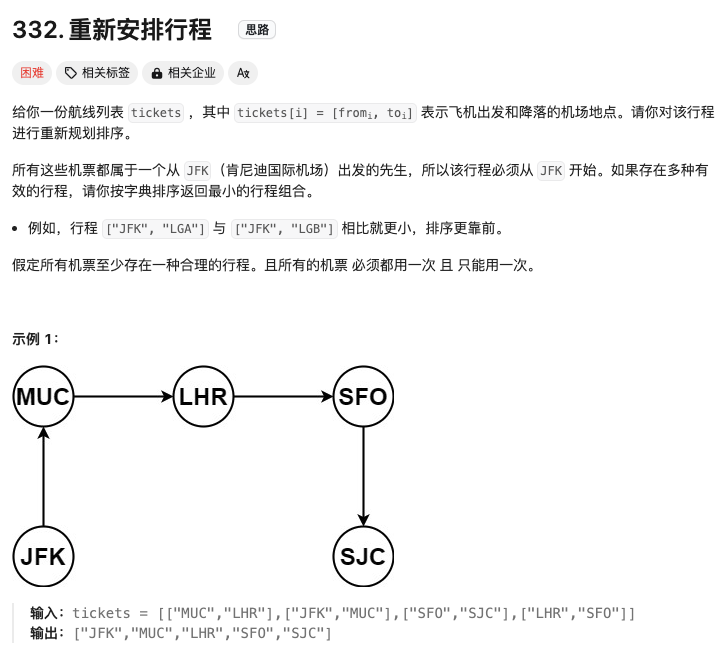
Click to expand the code。注意出发机场和到达机场是会重复的，搜索的过程没及时删除目的机场就会死循环。从而导致计算超时。因此需要剪枝策略检查是否前后两个的机票一模一样。其次，通过预先的排序也可以保证输出的结果字典序最小，而不是全部算完再排序～

回溯算法解二叉树类题目

毕竟回溯算法也是递归的一种，而递归算法在二叉树类题目中非常常见，因此回溯算法也常用于解决二叉树类题目。详细请见博客^Link

总结：回溯算法与递归算法的区别

回溯算法模板的核心是在递归前做选择，递归后撤销选择。两者是很像的。个人觉得回溯可以看出是递归的一种。
而对于二叉树中的递归（DFS）回溯算法的关注点在「树枝」，DFS 算法的关注点在「节点」。如下代码所示。直观理解就是回溯的前序和后序操作在for循环内，而DFS的前序和后序操作在for循环外。


// 回溯算法框架模板
void backtrack(...) {
    if (到达叶子节点) {
        return;
    }

    for (int i = 0, i < n; i++) {
        // 做选择
        ...

        backtrack(...)

        // 撤销选择
        ...
    }
}


// DFS 算法框架模板
void dfs(...) {
    if (到达叶子节点) {
        return;
    }
    // 做选择
    ...
    for (int i = 0, i < n; i++) {
        dfs(...)
    }
    // 撤销选择
    ...
}

回溯与二叉树的递归

回溯算法和二叉树的递归（DFS）算法的细微差别是：回溯算法是在遍历「树枝」，DFS 算法是在遍历「节点」。通过下题来理解这个观点：
给定一棵二叉树，搜索并记录所有值为 7 的节点，请返回节点列表。对于此题，如果直接用二叉树的递归遍历，代码如下：

在二叉树中搜索所有值为 7 的节点，请返回根节点到这些节点的路径：

进一步地，回溯问题通常包含一个或多个约束条件，约束条件通常可用于“剪枝”。
在二叉树中搜索所有值为 7 的节点，请返回根节点到这些节点的路径，并要求路径中不包含值为 3 的节点。

回溯算法 (backtracking algorithm)