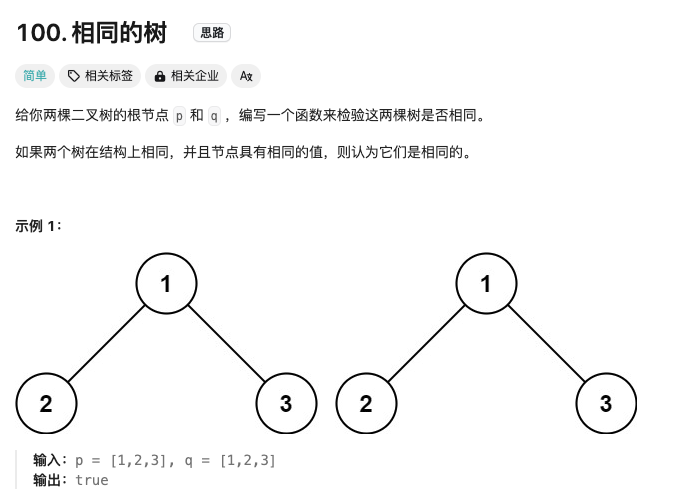
递归问题的关键点:问题的分解以及每个子问题的求解(其他的节点不用你操心,递归函数会帮你在所有节点上执行相同的操作。)
对于每个子问题采用已知上一个子问题的结果的前提下,求解当前子问题的结果。
每次写递归,都应该按照下面三要素:
链表类题目用递归的方法解决
大部分的链表类题目其实都可以用递归来解决的。详细请见链表类题目的汇总。请见博客Link
二叉树的遍历也是递归
回溯算法其实也就是递归算法
请见博客Link关于回溯算法的介绍
其他有意思的递归类题目汇总
外观数列
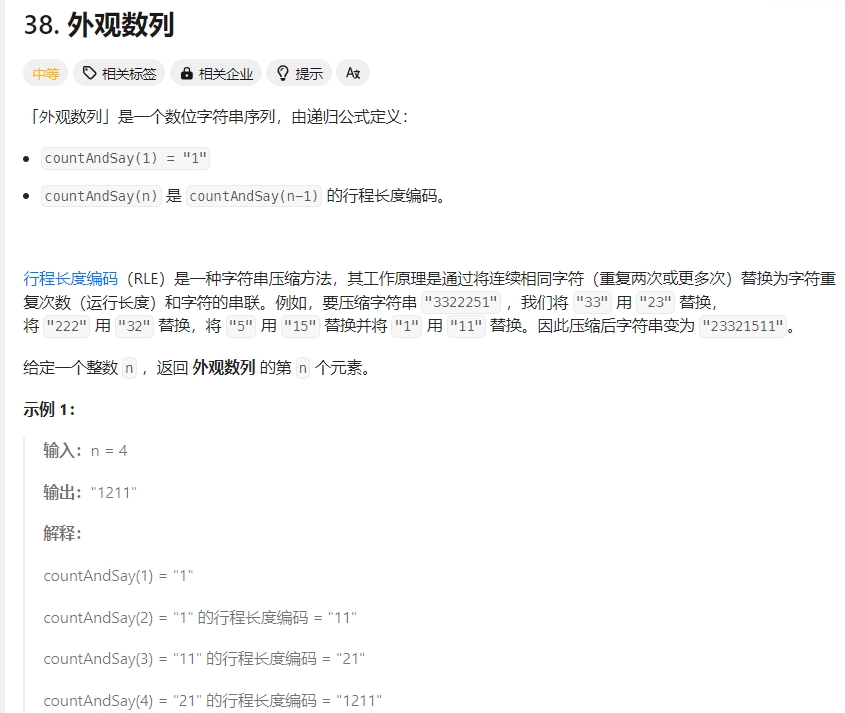
采用递归的解法:由于递归中带有for循环,时间复杂度为O(N2),空间复杂度为递归的栈空间
class Solution {
public:
string countAndSay(int n) {
if(n==1)
return "1";
string input_str=countAndSay(n-1);//每次输入的为上一个的结果
//由于需要基于上一次的结果做处理,为此,需要放在后序的位置上
int temp_num=1;//初始化为1(多少个1)
char temp_char=input_str[0];//第一个数
string result;
for(int i=1;i<input_str.size();i++)
{
if(input_str[i]==temp_char)//还是等于结果的
{
temp_num++;//记录多少个这个数
}
else
{
//结果记录为=现有结果+多少个当前字符+当前字符
result=result+to_string(temp_num)+temp_char;
//然后重置一下
temp_char=input_str[i];//新的字符
temp_num=1;//当前为1个
}
}
//根据for的终止条件,确定最后一个是否需要补上
//(把最后漏掉的,补上)
result=result+to_string(temp_num)+temp_char;
return result;
}
};
由于数量只有30个,还有一种解法是打表直接输出全部结果😂,时间复杂度为O(1),空间复杂度为O(C×M)。其中 C 是 N 是上界,在本题中 C=30,M 为生成的字符串中的最大长度。
但类似这种可以拆分为子问题的解题思路最直接其实还是递归~
统计每个月兔子的总数
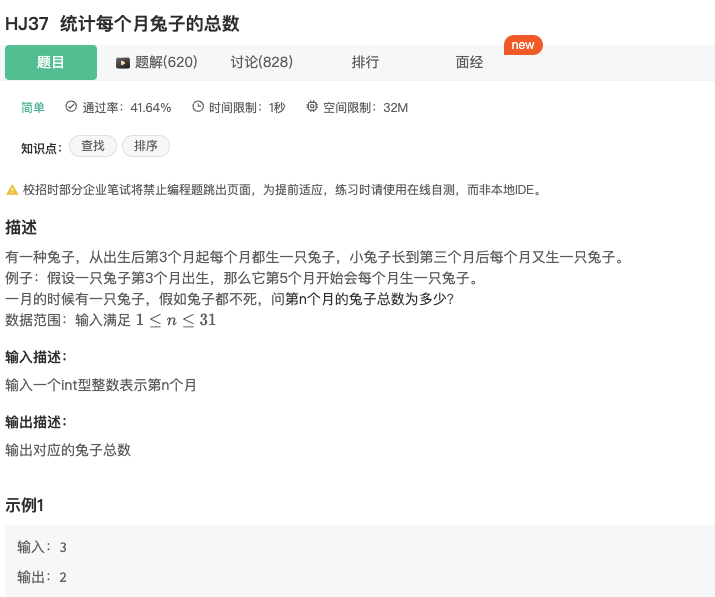
Click to expand the code
上面递归算法的思路有点不是太直接,也可以采用下面直接计算
迷宫问题
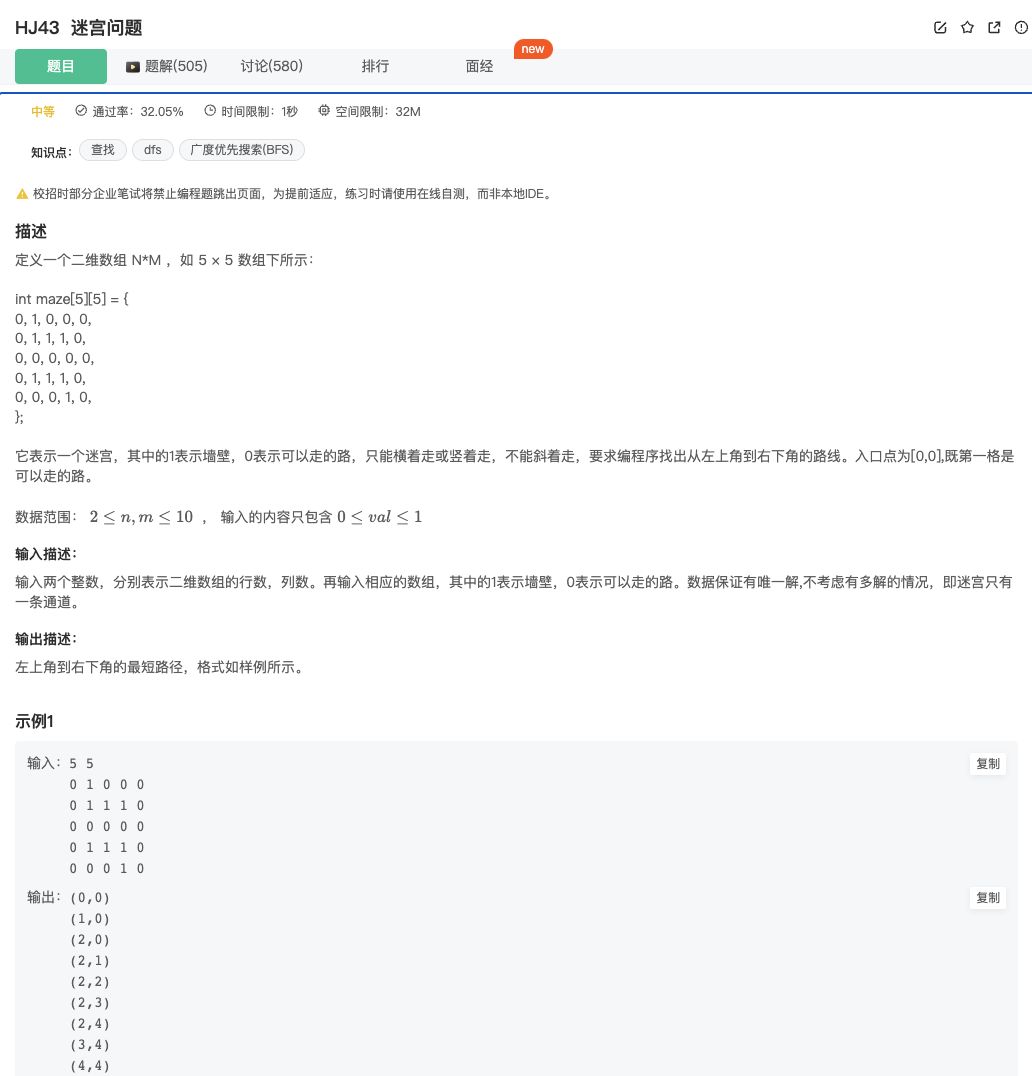
Click to expand the code
Click to expand the code(跟上面解法本质一样的~)
放苹果
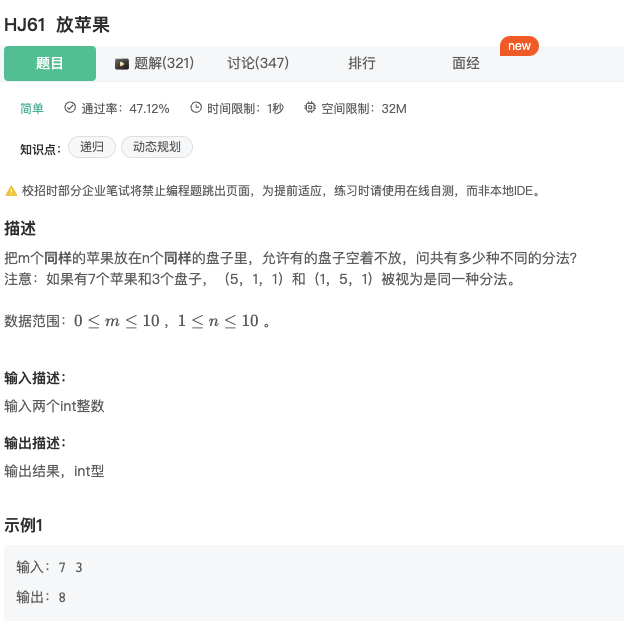
Click to expand the code
24点游戏算法
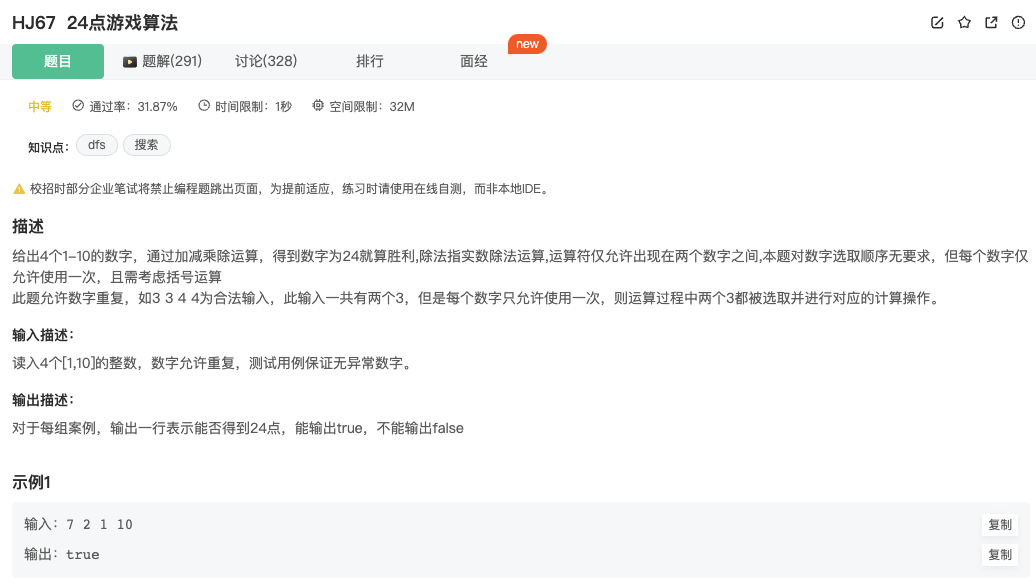
Click to expand the code。vector删除中间某个元素:rest.erase(rest.begin() + i)
数组分组
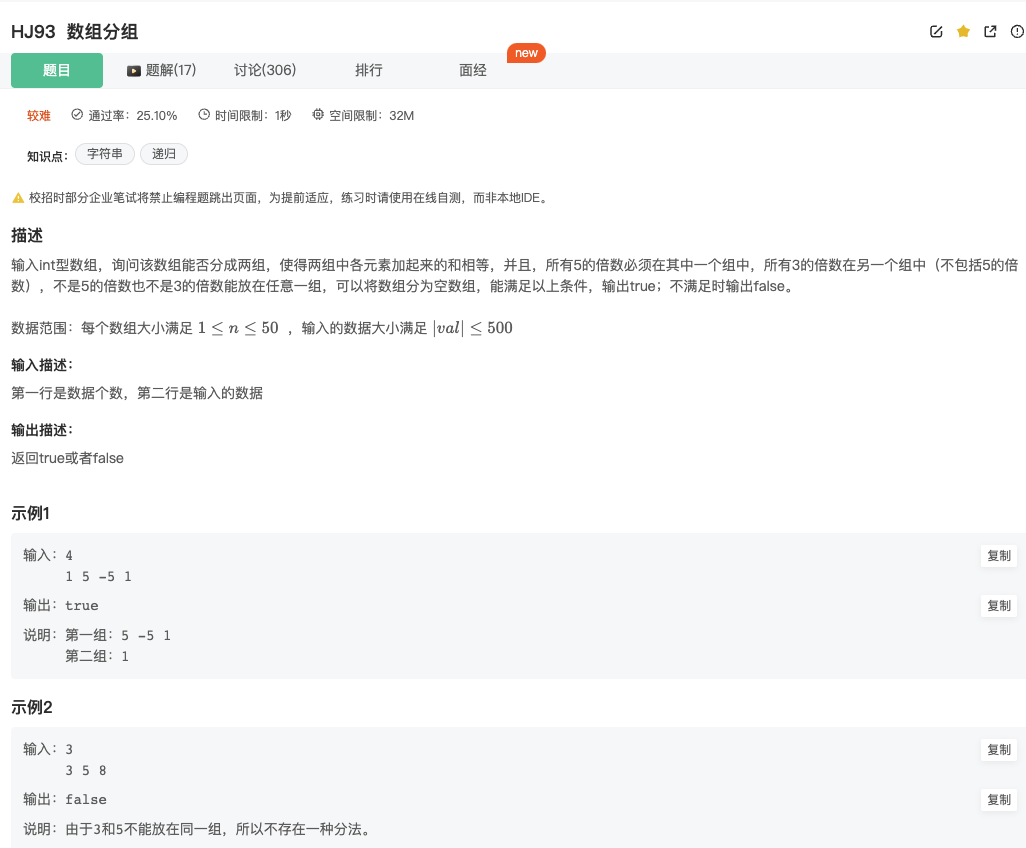
Click to expand the code.关键是分解问题的思路~
杨辉三角
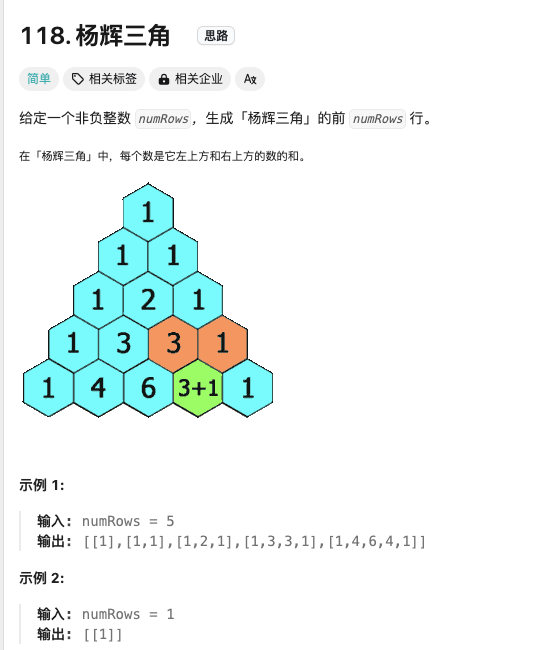
Click to expand the code。大部分的解法都是直接给出二维矩阵,然后逐步推算,但是个人觉得递归的思路更直接~后序遍历