What is Diffusion and Deep Generative Modeling

2025-03-16

引言

之前博客学习了什么是Transformer,在被其强大的性能所震惊的同时，又想起生成类AI中，扩散模型(Diffusion Model)也是非常关键的。 为此写下本博文来对其进行学习。本博文大部分内容来源于网络博客，在文末标出参考。

本博文仅供本人学习记录用

图像生成

首先先了解下神经网络是如何生成图像的。

为了生成丰富且随机的图像，一个图像生成AI要根据随机数来生成图像。 而这个随机数是需要满足标准正态分布的随机向量。这样，每次要生成新图像时，只需要从标准正态分布里随机生成一个向量并输入给AI就行了。

而AI程序中，负责生成图像的是一个神经网络模型，网络需要从数据中学习。 对于图像生成任务，网络的训练数据一般是同类型的图片。如绘制人脸的神经网络就会用人脸照片来训练。那么神经网络会学习如何把一个随机向量映射成一张图片，并确保这个图片和训练集的图片是一类图片。

图像生成网络会学习如何把一个向量映射成一幅图像。设计网络架构时，最重要的是设计学习目标，让网络生成的图像和给定数据集里的图像相似。

但生成任务的一个难点就是：缺乏有效的指导。因为对于一般的learning任务，训练集有标准的答案，网络学习的只是如何让预测更靠近标准答案。但是生成类任务是没有标准答案的。

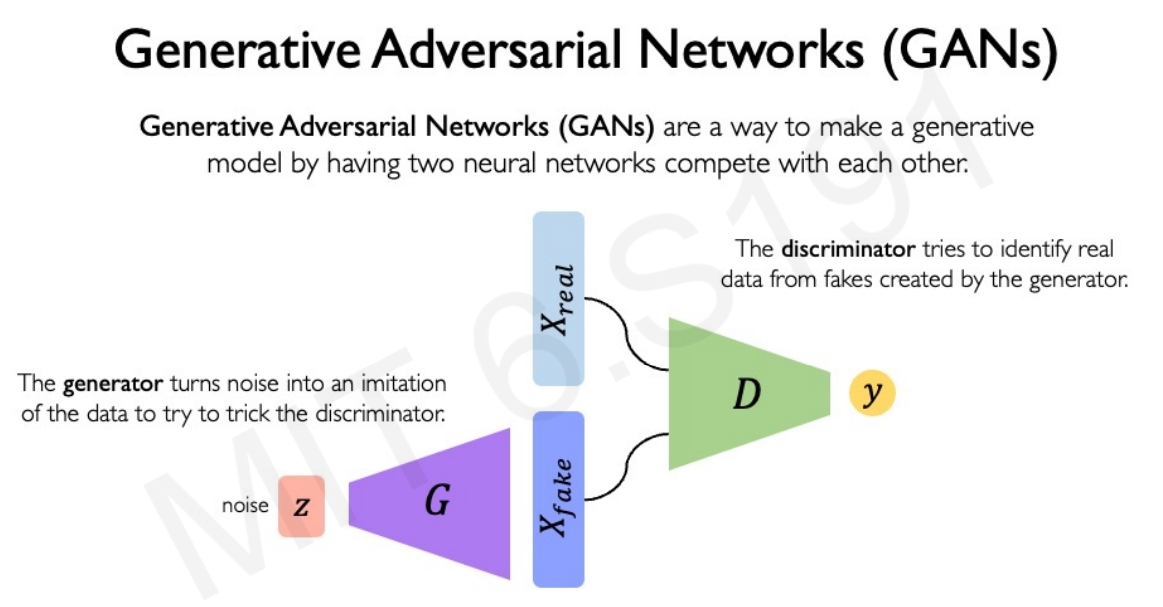
为了解决这一问题，人们专门设计了一些用于生成图像的神经网络架构。如生成对抗模型（Generative adversarial network, GAN）和变分自编码器（Variational Autoencoder, VAE）。

GAN

GAN基本思路是，既然生成网络（生成器）无法知道一幅图片好不好，那么就再训练一个网络（对抗网络/判别器），用于辨别生成网络生成的图片是不是和训练集里的图片长得一样（或者分布一样）。两个网络互相对抗，共同进步。

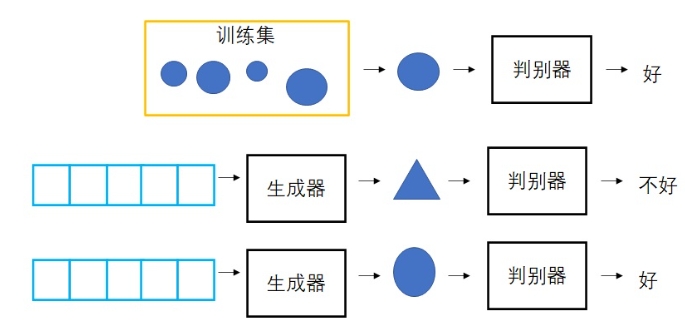
VAE

VAE的基本思路则是：既然用向量来生成合适的图像很困难，那么就同时学习怎么用图像生成向量。 这样，把某图像变成向量，再用该向量生成图像，就应该得到一幅和原图像一模一样的图像。 而每一个向量的绘画结果有了一个标准答案，可以用一般的优化方法来指导网络的训练了。 VAE中，把图像变成向量的网络叫做编码器，把向量转换回图像的网络叫做解码器。而最终，解码器就是负责生成图像的模型。

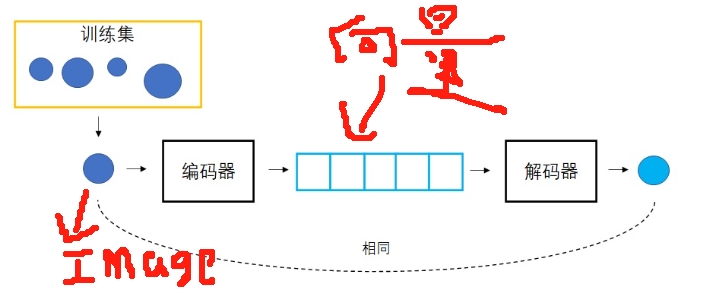
Diffusion Model

Diffusion模型的思路则是：一个分布可以通过不断地添加噪声变成另一个分布。 那么在图像生成任务里面，可以理解为：来自训练集的图像可以通过不断添加噪声变成符合标准正态分布的图像。

那么基于这个概念，可以将VAE做进一步修改：

  1. 不再训练一个可学习的编码器，而是把编码过程改为不断添加噪声的过程；
  2. 那么也就不再需要把图像压缩成的向量，而是自始至终都对图像做操作。
  3. 解码器依然是一个可学习的神经网络，它的目的也同样是实现编码器的逆操作。不过，既然编码过程变成了加噪，那么解码器就应该负责去噪。而对于神经网络来说，去噪任务学习起来会更加有效（low-level vision）。因此，扩散模型既不会涉及GAN中复杂的对抗训练，又比VAE更强大。

具体地，在Diffusion model中，编码和解码称伟正向过程和逆向过程。如下图所示。 在正向过程中，输入的图片$X_{0}$会不断混入高斯噪声。经过$T$次加噪声操作后，得到图像$X_{T}$，其为一幅符合标准正态分布的纯噪声图像。 而在反向过程中，我们希望训练出一个神经网络，该网络能够学会$T$个去噪声操作，把图像$X_{T}$还原回$X_{0}$。 网络的学习目标是让$T$个去噪声操作正好能抵消掉对应的加噪声操作。

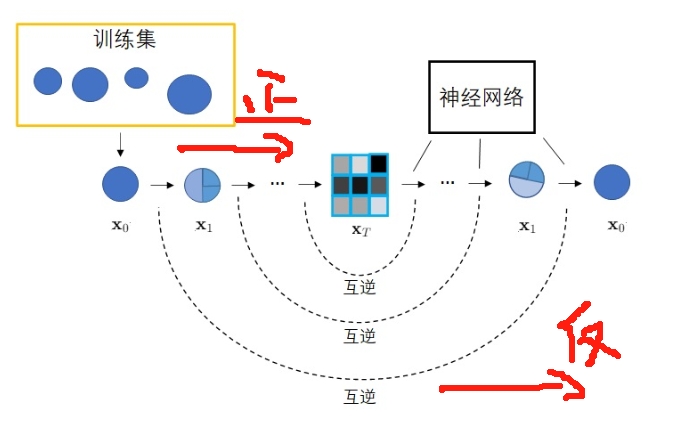
训练完毕后，只需要从标准正态分布里随机采样出一个噪声，再利用反向过程里的神经网络把该噪声恢复成一幅图像，就能够生成一幅图片了。如下图所示。

下图为不同种类的生成模型的总结对比

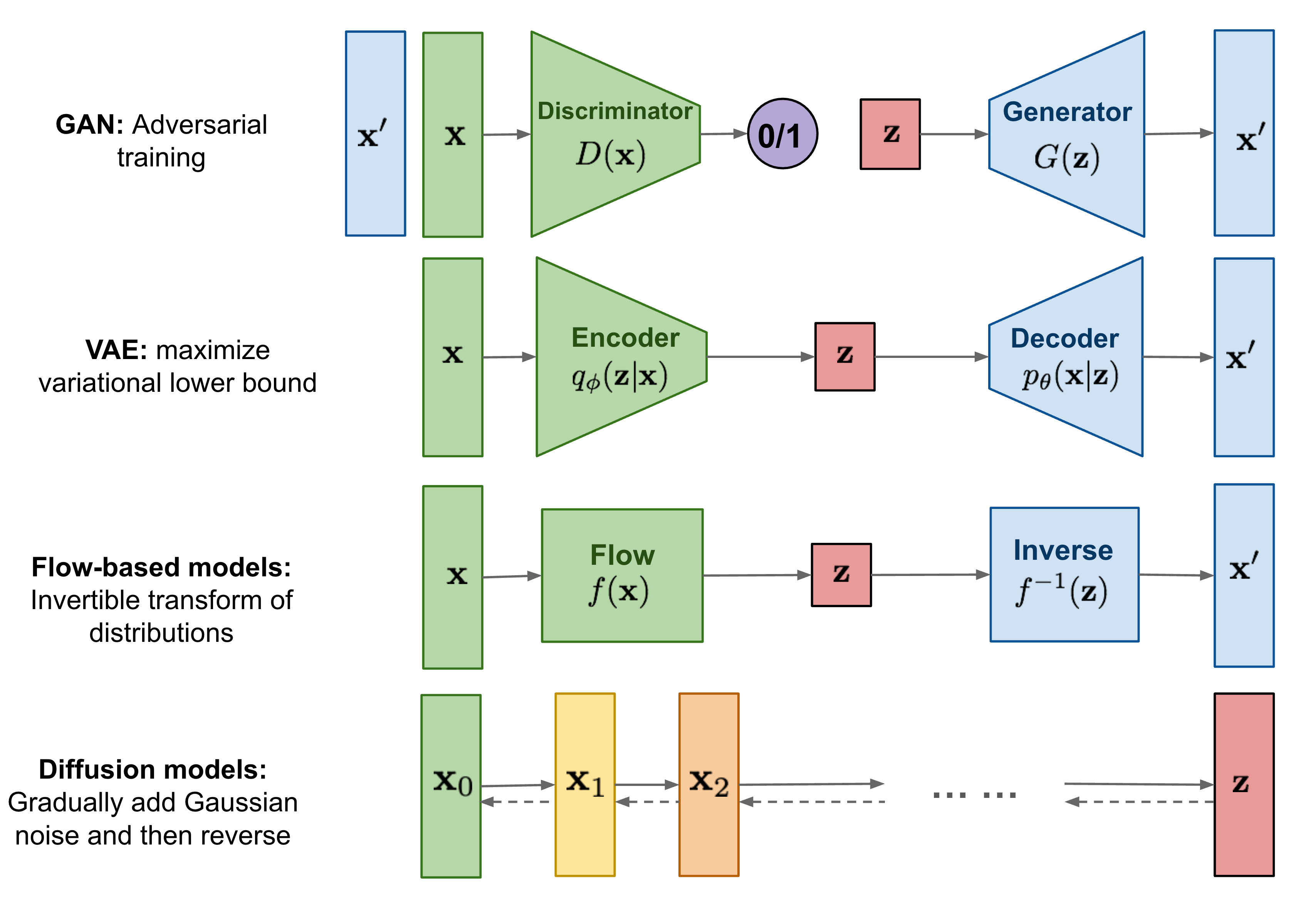
Deep Generative Modeling

补充《MIT Introduction to Deep Learning》课程，其中第四节对生成模型进行了介绍。课程对应的PPT如下

生成模型的发展非常强大，比如下面三张图片，竟然都是生成的

生成模型最基本的原理是：从训练样本中学到某种分布，让模型可以输出该分布的数据。Take as input training samples from some distribution and learn a model that represents that distribution

Autoencoders，其实就是类似U-Net的结构，从输入的数据$x$中学习低维度的latent space $z$,通过将$z$ mapping back回原来的数据，即可实现自监督/un-supervise learning，不需要任何的label

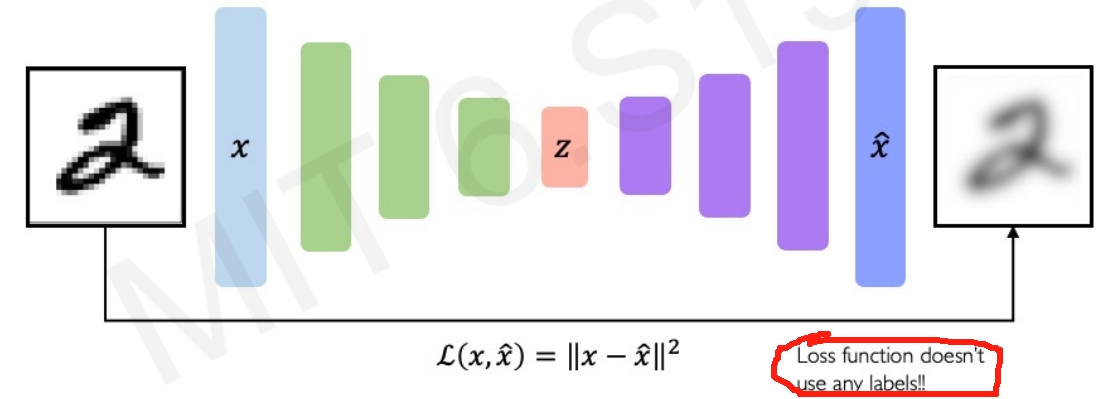
这个过程实际上就是让网络去学习压缩的latent representation，而重建的loss则是强迫所学习的latent representation可以编码更多信息，因此这个Autoencoders的框架可以理解为Autoencoding = Automatically encoding data; "Auto" = self-encoding

而更常用的则是Variational Autoencoders (VAES)，也就是引入多样性来提升它的泛化能力。如下图所示.

对于传统的Autoencoders，是确定性模型，也就是对于输入，理论上会获得相同的输出（也就是它是一个deterministic encoding）。 因此需要引入一些随机性（randomness）到Autoencoders中

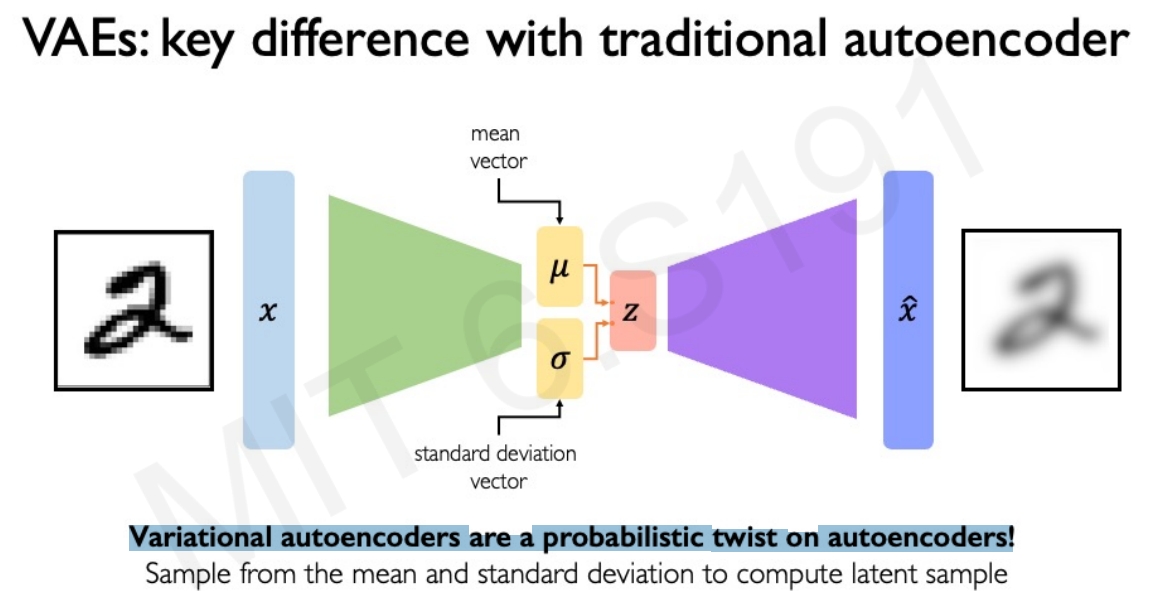
对于每个latent variables都添加一个概率分布。那么进一步可以理解为编码器和解码器都是学习概率分布。而两个network分别学习权重$\phi$和$\theta$

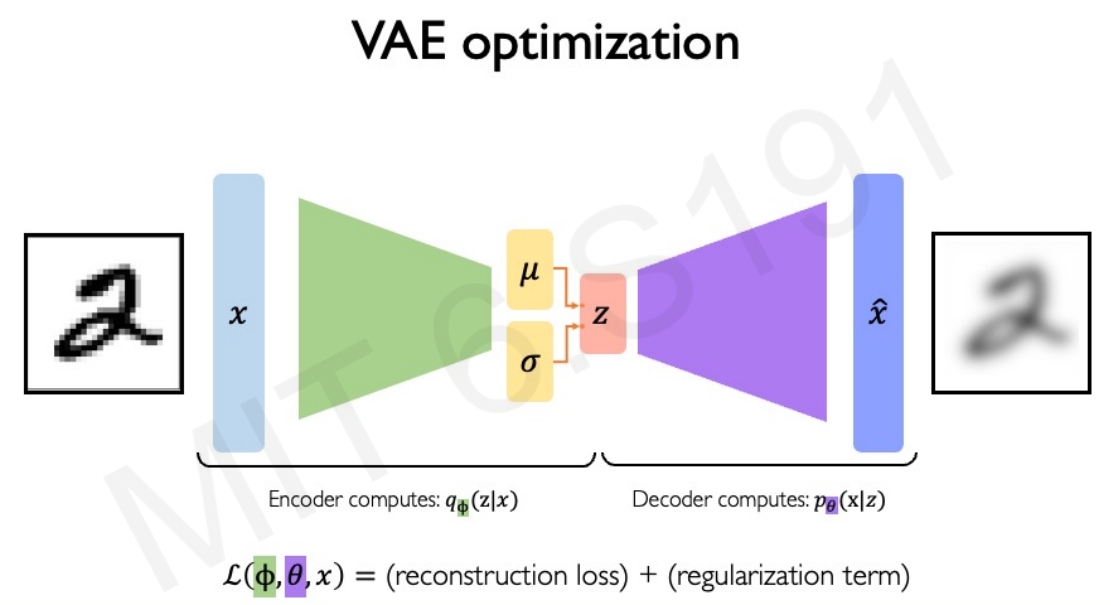
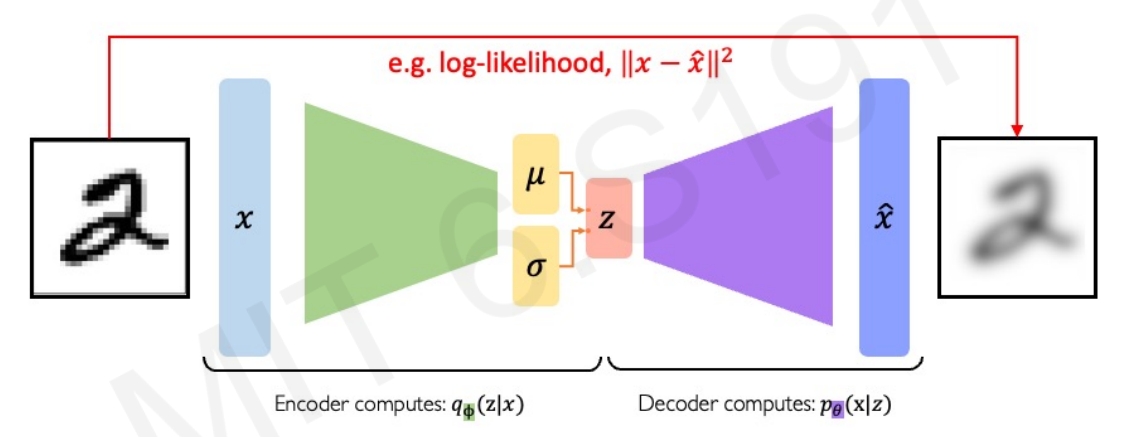重构loss 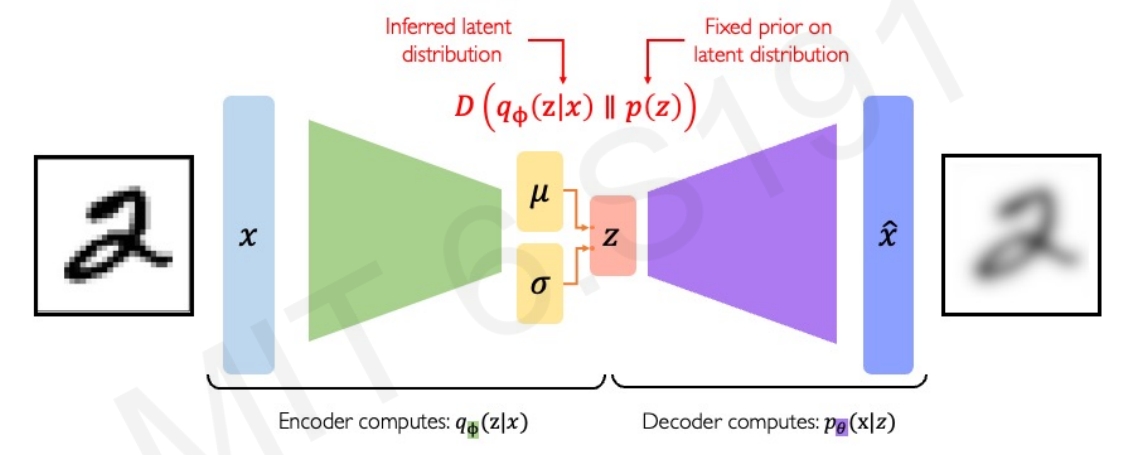正则化loss

而所谓的正则化loss实际上就是让学习的分布要更加接近于某种预定义的分布。如下图所示，假设需要latent的先验分布为正态分布 而下方图片则是计算两个分布有多靠近的公式

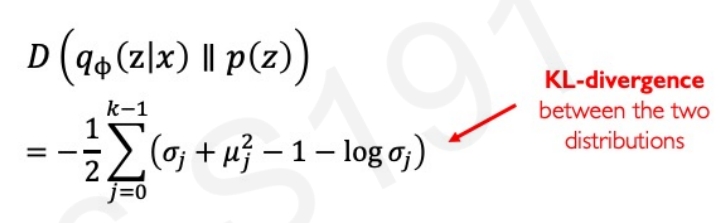
而之所以要这样的正则化处理，是因为需要让网络学习的分布要跟预定义的一样，要”meaningful”.

然而对于BP算法而言，需要网络是确定性的，随机的是没有办法反向传播梯度来更新权重的，因此需要对其sampling layer进行参数化如下：

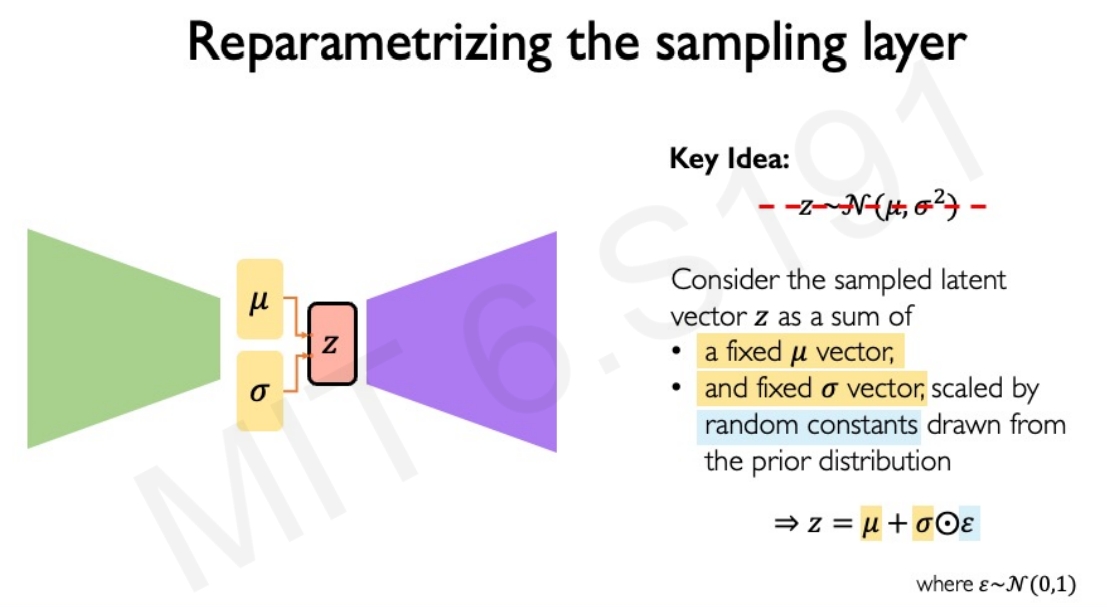
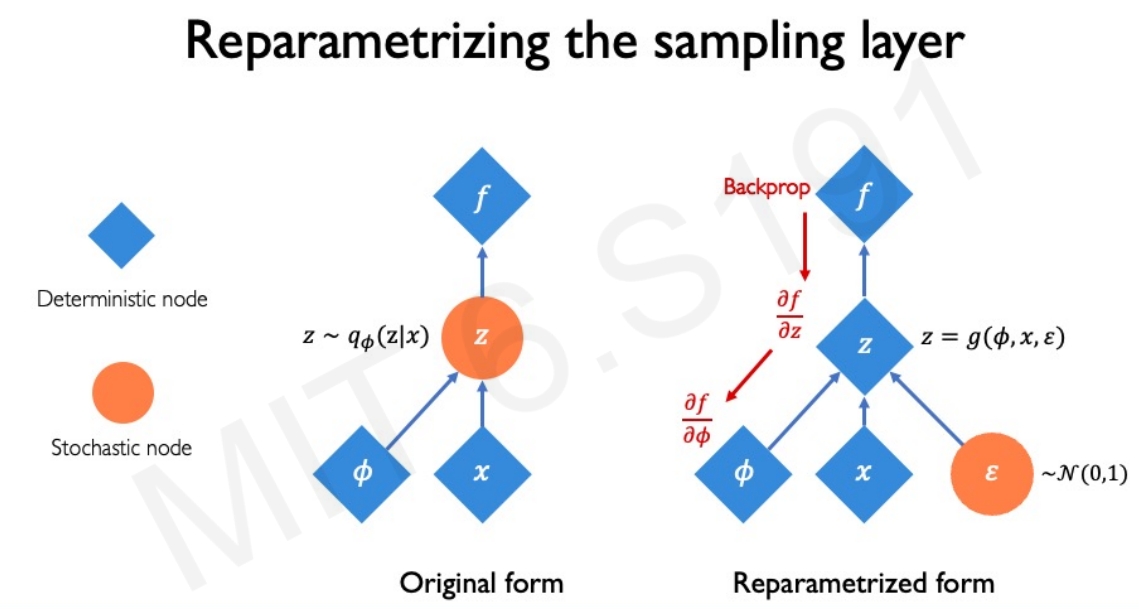
此处深入学习VAE是因为其跟diffusion模型的思路是非常像的，而对于GAN网络，此处就不介绍了~

Diffusion的基本思路

Diffusion模型的思路则是：一个分布可以通过不断地添加噪声变成另一个分布。如下图所示

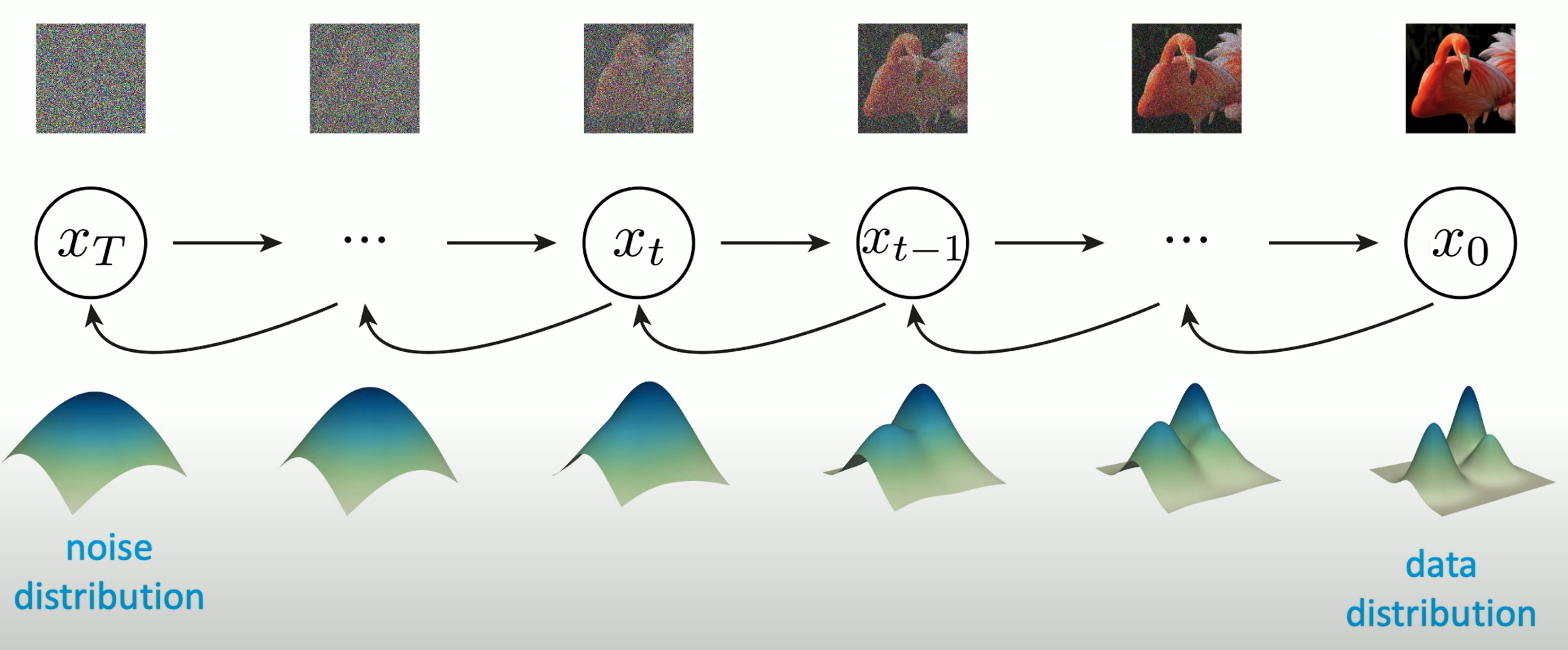
Forward diffusion process

在正向过程中，来自训练集的图片$X_{0}$会加入$T$次噪声，使得最终得到图像$X_{T}$为符合标准正态分布。 准确来说，加噪声并不是给上一时刻的图像加上噪声值，而是从一个均值与上一时刻图像相关的正态分布里采样出一幅新图像。直观解析通过下面公式来表述：

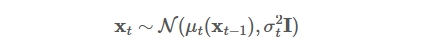
其中$X_{t-1}$为上一时刻的图像，$X_{t}$为当前加了噪声后生成的图像。可以理解为它是从一个均值为$X_{t-1}$的正态分布中采样出来的。

PS：这个过程也符合马尔可夫过程，因为当前状态仅仅由上一状态决定，不会由更早的状态决定。

而为了让每一步加噪声的过程能够从慢到快改变原图像，让最终的图像$X_{T}$为均值0，方差$I$(标准正态分布)，那么加噪声的扩散模型会设置为：

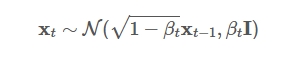
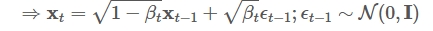
具体的推导为什么是$1-\beta$的形式请见Link

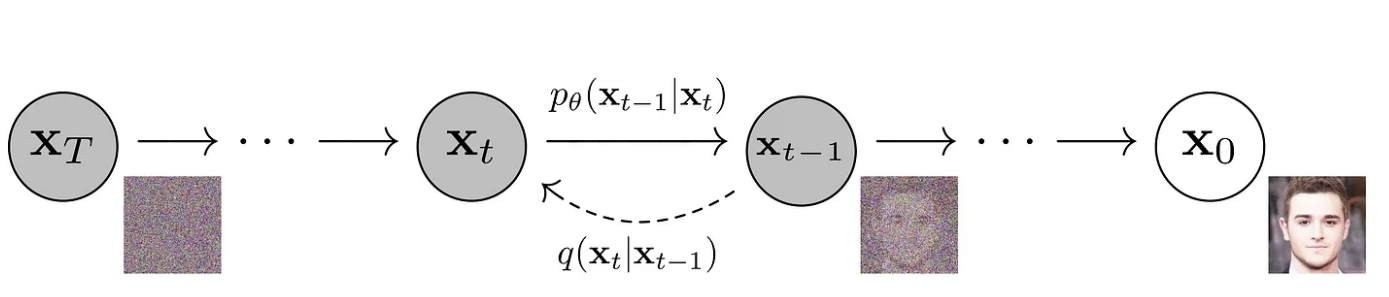
Reverse diffusion process

在正向过程中，人为设置了$T$步加噪声过程。而在反向过程中，则是希望能够倒过来取消每一步加噪声操作，让一幅纯噪声图像变回数据集里的图像。 这样，利用这个去噪声过程，就可以把任意一个从标准正态分布里采样出来的噪声图像变成一幅和训练数据长得差不多的图像，从而起到图像生成的目的。

而对于上述正向过程的$\beta_{t}$只要足够的小，那么每一步加噪声的逆操作也会满足正态分布

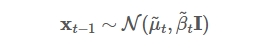
而当前时刻加噪声的逆操作的均值$\tilde{\mu}{t}$和方差$\tilde{\beta}{t}$则是由当前的时刻$t$和当前的图像$X_{t}$来决定。 网络应该就是输入$t$和$X_{t}$拟合获得当前的均值$\tilde{\mu}{t}$和方差$\tilde{\beta}{t}$。而它的均值的求解过程请见Link，下面直接给出结果

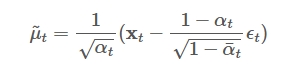
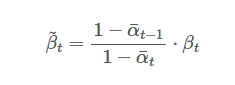
给定某个输入时，去噪的正态分布的均值和方差是可以用解析式表达出来的

$\beta_{t}$为加噪声的方差，是一个常量。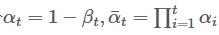 而$\varepsilon_{t}$则是前面正向过程的时候从对应的$\varepsilon$(注意下面时间表达差一个时刻):

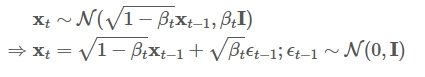
对于神经网络拟合均值的时候，$x_{t}$为已知，，那么上面公式中就只有 $\varepsilon_{t}$ 是不确定的，那么网络实际上只需要预测方差 $\varepsilon_{t}$ 即可获得对应的去噪的均值 $\tilde{\mu}{t}$ 和方差 $\tilde{\beta}{t}$。

对于网络预测的$\varepsilon_{\theta}(x_{t},t)$($\theta$为网络可学习参数)，让其和生成$x_{t}$的时候用的噪声方差$\tilde{\beta}_{t}$的均方误差最小即可：

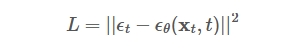
各类型的Diffusion Models

DDPM

噪扩散概率模型（Denoising Diffusion Probabilistic Models, DDPM），也就是上文介绍的diffusion Model了. 它的采样速度非常慢，因为DDPM在采样时通常要做1000次去噪操作。 但对于实际的基于扩散模型的图像生成应用基本都只需要20次左右的去噪操作即可生成图像，而这些方法用得则是DDIM。

DDIM

基于DDPM，DDIM（Denoising Diffusion Implicit Model, 去噪扩散隐式模型）论文主要提出了两项改进：

  1. 对于一个已经训练好的DDPM，只需要对采样公式做简单的修改，模型就能在去噪时「跳步骤」，在一步去噪迭代中直接预测若干次去噪后的结果。
  2. 推广了DDPM的数学模型，从更高的视角定义了DDPM的前向过程（加噪过程）和反向过程（去噪过程）。在这个新数学模型下，可以自定义模型的噪声强度，让同一个训练好的DDPM有不同的采样效果。

参考资料